
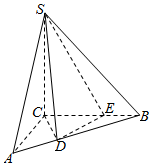
 如图,在三棱锥S-ABC中,SC⊥平面ABC,SC=3,AC⊥BC,CE=2EB=2,AC=$\frac{3}{2}$,CD=ED.
如图,在三棱锥S-ABC中,SC⊥平面ABC,SC=3,AC⊥BC,CE=2EB=2,AC=$\frac{3}{2}$,CD=ED.分析 (Ⅰ)建立坐标系,求出向量的坐标,得到DE⊥CD,DE⊥CS,求出线面垂直即可;
(Ⅱ)设平面SAD的法向量为$\overrightarrow{n}$=(x,y,z),求出一个法向量,代入余弦公式即可求出余弦值;
(Ⅲ)作AH⊥平面SCD,垂足为H,求出$\overrightarrow{AH}$的坐标,从而求出点A到平面SCD的距离.
解答 解:如图示: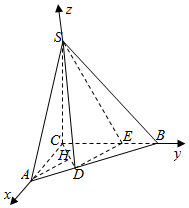 ,
,
以C为原点建立空间直角坐标系,
由题意得:A($\frac{3}{2}$,0,0),C(0,0,0),D(1,1,0),E(0,2,0),S(0,0,3),
(Ⅰ)证明:∵$\overrightarrow{DE}$=(-1,1,0),$\overrightarrow{CD}$=(1,1,0),$\overrightarrow{CS}$=(0,0,3),
∴$\overrightarrow{DE}$•$\overrightarrow{CD}$=-1+1+0=0,$\overrightarrow{DE}$•$\overrightarrow{CS}$=0+0+0=0,
即DE⊥CD,DE⊥CS,
∵CD∩CS=C,
∴DE⊥平面SCD;
(Ⅱ)解:由(Ⅰ)可得$\overrightarrow{DE}$=(-1,1,0)为平面SCD的一个法向量,
设平面SAD的法向量为$\overrightarrow{n}$=(x,y,z),
而$\overrightarrow{AD}$=(-$\frac{1}{2}$,1,0),$\overrightarrow{AS}$=(-$\frac{3}{2}$,0,3),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AD}=0}\\{\overrightarrow{n}•\overrightarrow{AS}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-\frac{1}{2}x+y=0}\\{-\frac{3}{2}x+3z=0}\end{array}\right.$,
不妨设x=2,可得$\overrightarrow{n}$=(2,1,1),
易知二面角A-SD-C为锐角,
因此有|cos<$\overrightarrow{DE}$,$\overrightarrow{n}$>|=$|\frac{-2+1+0}{\sqrt{2}•\sqrt{6}}|$=$\frac{\sqrt{3}}{6}$,
即二面角A-SD-C的余弦值是$\frac{\sqrt{3}}{6}$;
(Ⅲ)解:$\overrightarrow{AC}$=(-$\frac{3}{2}$,0,0),$\overrightarrow{AD}$=(-$\frac{1}{2}$,1,0),$\overrightarrow{AS}$=(-$\frac{3}{2}$,0,3),
作AH⊥平面SCD,垂足为H,
设$\overrightarrow{AH}$=x$\overrightarrow{AC}$+y$\overrightarrow{AD}$+z$\overrightarrow{AS}$=(-$\frac{3}{2}$x-$\frac{1}{2}$y-$\frac{3}{2}$z,y,3z),且x+y+z=1,
由$\overrightarrow{AH}$⊥$\overrightarrow{CD}$,$\overrightarrow{AH}$⊥$\overrightarrow{CS}$,得:
$\left\{\begin{array}{l}{-\frac{3}{2}x-\frac{1}{2}y-\frac{3}{2}z+y=0}\\{9z=0}\\{x+y+z=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{1}{4}}\\{y=\frac{3}{4}}\\{z=0}\end{array}\right.$,
∴$\overrightarrow{AH}$=(-$\frac{3}{4}$,$\frac{3}{4}$,0),|$\overrightarrow{AH}$|=$\frac{3\sqrt{2}}{4}$,
即点A到平面SCD的距离是$\frac{3\sqrt{2}}{4}$.
点评 本题考查了线面垂直,考查平面的法向量,点到平面的距离,是一道中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 不存在x∈R,2x4-x2+1<0 | B. | 存在x∈R,2x4-x2+1<0 | ||
| C. | 对任意的x∈R,2x4-x2+1≥0 | D. | 存在x∈R,2x4-x2+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
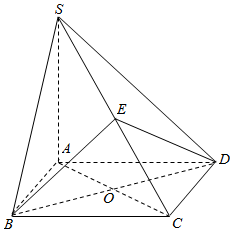 如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.
如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -ln2-1 | B. | -1+ln2 | C. | -ln2 | D. | ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
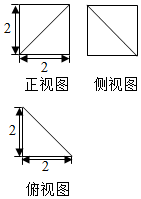
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤1 | B. | -$\frac{1}{3}$≤a≤1 | C. | a>1 | D. | a≥-$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 540种 | B. | 270种 | C. | 180种 | D. | 90种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com