
 在长方体ABCD-A1B1C1D1中,AB=3,AD=2,CC1=1,一条绳子从点A沿表面拉到点C1,求绳子的最短的长.
在长方体ABCD-A1B1C1D1中,AB=3,AD=2,CC1=1,一条绳子从点A沿表面拉到点C1,求绳子的最短的长. 分析 根据题意,画出三种展开的图形,求出A、C1两点间的距离,比较大小,从而找出最小值即为所求.
解答 解:①沿平面A A 1B 1B、平面 A 1B 1C 1D 1铺展成平面,此时 AC 1=$\sqrt{{3}^{2}+(1+2)^{2}}$=3$\sqrt{2}$.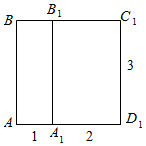
②沿平面 AA 1D 1D、平面 A 1D 1C 1B 1铺展成平面,此时 AC 1=$\sqrt{{2}^{2}+(1+3)^{2}}$=2$\sqrt{5}$.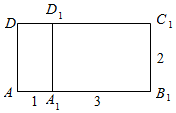
③沿平面 AA 1B 1B、平面 BB 1C 1C铺展成平面,此时 AC 1=$\sqrt{{1}^{2}+(3+2)^{2}}$=2$\sqrt{6}$.
故绳子的最短的长为3$\sqrt{2}$.
点评 本题考查棱柱的结构特征,考查分类讨论思想,考查计算能力,属于中档题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
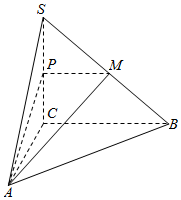 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
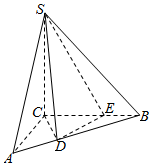 如图,在三棱锥S-ABC中,SC⊥平面ABC,SC=3,AC⊥BC,CE=2EB=2,AC=$\frac{3}{2}$,CD=ED.
如图,在三棱锥S-ABC中,SC⊥平面ABC,SC=3,AC⊥BC,CE=2EB=2,AC=$\frac{3}{2}$,CD=ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
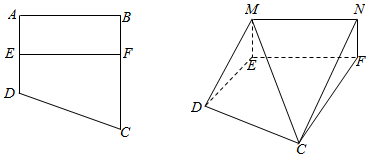
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
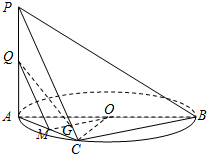 如图,PA垂直圆O所在的平面,C是圆O上的点,Q为PA的中点,G为△AOC的重心,AB是圆O的直径,且AB=2AC=2.
如图,PA垂直圆O所在的平面,C是圆O上的点,Q为PA的中点,G为△AOC的重心,AB是圆O的直径,且AB=2AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0)∪(2,+∞) | B. | (-2,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com