
分析 由基本不等式求最值的规则,逐个验证可得.
解答 解:由0<x<$\frac{1}{2}$可得0<1-2x<1,
∴y=x(1-2x)=$\frac{1}{2}$•2x•(1-2x)≤$\frac{1}{2}$($\frac{2x+1-2x}{2}$)2=$\frac{1}{8}$,
当且仅当2x=1-2x即x=$\frac{1}{4}$时取等号,
故函数$y=x(1-2x)(0<x<\frac{1}{2})$有最大值为$\frac{1}{8}$,①正确;
∵x<0,∴-x>0,∴y=2-3x-$\frac{4}{x}$=2+[(-3x)+($\frac{4}{-x}$)]
≥2+2$\sqrt{(-3x)•\frac{4}{-x}}$=2+4$\sqrt{3}$,当且仅当(-3x)=($\frac{4}{-x}$)即x=$\frac{2\sqrt{3}}{3}$时取等号,
故函数y=2-3x-$\frac{4}{x}$(x<0)有最小值2+4$\sqrt{3}$,②错误;
∵a>0,∴(1+a)(1+$\frac{1}{a}$)=2+a+$\frac{1}{a}$≥2+2$\sqrt{a•\frac{1}{a}}$=4
当且仅当a=$\frac{1}{a}$即a=1时取等号,故③正确;
故答案为:①③
点评 本题考查基本不等式,逐个验证是解决问题的关键,属基础题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:选择题
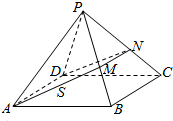 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )| A. | 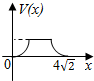 | B. | 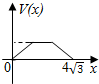 | C. | 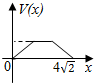 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 2或4 | D. | 4或8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com