
如图,三棱锥P ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点 
(1)若PA=2,求直线AE与PB所成角的余弦值;
(2)若PA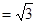 ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC
(1)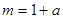 ,
,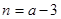 ;(2)
;(2)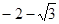
解析试题分析:(1)首先建立空间直角坐标系,给出相关点的坐标,利用空间向量求解;(2) 利用空间向量求解平面的法向量,然后根据法向量互相垂直可证明
试题解析:(1)如图,取AC的中点F,连接BF,则BF⊥AC 以A为坐标原点,过A且与FB平行的直线为x轴,AC为y轴,AP为z轴,建立空间直角坐标系 
则A(0,0,0),B(,1,0), C(0,2,0),P(0,0,2),E(0,1,1),
从而=(,1, 2), =(0,1,1)
设直线AE与PB所成角为θ,
则cosθ=||=
即直线AE与PB所成角的余弦值为 5分
(2)如上图,则
A(0,0,0),B(,1,0), C(0,2,0),P(0,0,),E(0,1,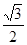 ),
),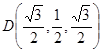
设平面PBC的法向量为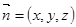 ,则
,则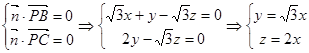
令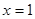 ,则
,则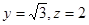 ,所以
,所以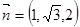
同理可求平面ADE的法向量
所以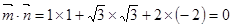 ,即
,即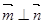
于是平面ADE⊥平面PBC
考点:空间直角坐标系、空间向量、线线角以及面面垂直的证明


科目:高中数学 来源: 题型:解答题
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.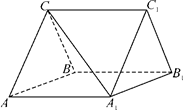
(Ⅰ)证明:AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥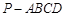 的底面是直角梯形,
的底面是直角梯形,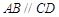 ,
,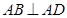 ,
,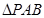 和
和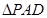 是两个边长为
是两个边长为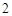 的正三角形,
的正三角形,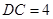 ,
, 为
为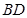 的中点,
的中点,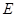 为
为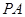 的中点.
的中点.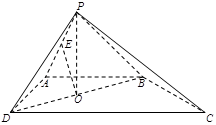
(Ⅰ)求证: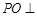 平面
平面 ;
;
(Ⅱ)求证: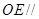 平面
平面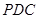 ;
;
(Ⅲ)求直线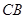 与平面
与平面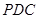 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com