
| A. | 若a5>0,则a2017<0 | B. | 若a6>0,则a2018<0 | ||
| C. | 若a5>0,则S2017>0 | D. | 若a6>0,则S2018>0 |
分析 利用等比数列的通项公式及其前n项和公式即可判断出正误.
解答 解:A.若a5=a1q4>0,则a2017=a1q2016>0,故本选项错误;
B、a6=a1q5>0,则a2018=a1q2017>0,故本选项错误;
C、a5=a1q4>0,则a1>0.若q=1时,S2017=2017a1>0;若q≠1,S2017=$\frac{{a}_{1}({q}^{2017}-1)}{q-1}$>0,故本选项正确;
D、若a6=a1q5>0.若a1>0,q=1时,S2018=2018a1>0;若q≠1,S2018=$\frac{{a}_{1}({q}^{2018}-1)}{q-1}$,当q<-1时,S2018<0,q=-1,S2018=0,故本选项错误;
故选:C.
点评 本题考查了等比数列的通项公式及其前n项和公式、不等式的性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3},+∞$) | B. | ($\frac{2}{3},1)$ | C. | (0,2) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
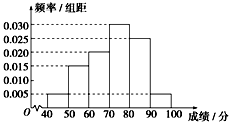 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}-\frac{1}{e}$ | B. | $-\frac{3}{2}-\frac{2}{e}$ | C. | $-\frac{3}{4}-\frac{1}{2e}$ | D. | $-1-\frac{1}{e}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com