
已知函数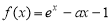 (e为自然对数的底数),a>0.
(e为自然对数的底数),a>0.
(1)若函数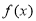 恰有一个零点,证明:
恰有一个零点,证明: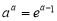 ;
;
(2)若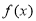 ≥0对任意x∈R恒成立,求实数a的取值集合.
≥0对任意x∈R恒成立,求实数a的取值集合.
(1)见解析;(2){1}.
【解析】
试题分析:(1)先判断f(x)的单调性,根据“f(x)前有一个零点”,找到关于a的等式,化简整理可得需证结论;(2)根据(1),只需f(x)的最小值不小于0即可.
试题解析:(1)证明: 由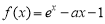 ,得
,得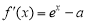 . 1分
. 1分
由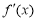 >0,即
>0,即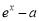 >0,解得x>lna,同理由
>0,解得x>lna,同理由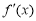 <0解得x<lna,
<0解得x<lna,
∴ f(x)在(-∞,lna)上是减函数,在(lna,+∞)上是增函数,
于是f(x)在x=lna取得最小值.
又∵ 函数f(x)恰有一个零点,则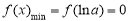 , 4分
, 4分
即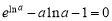 . 5分
. 5分
化简得: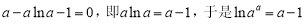 ,
,
∴ 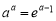 . 6分
. 6分
(2)【解析】
由(1)知,f(x)在x=lna取得最小值f(lna),
由题意得f(lna)≥0,即a-alna-1≥0, 8分
令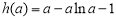 ,则
,则 ,
,
由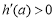 可得0<a<1,由
可得0<a<1,由 可得a>1.
可得a>1.
∴ h(a)在(0,1)上单调递增,在(1,+∞)上单调递减,即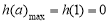 ,
,
∴ 当0<a<1或a>1时,h(a)<0,
∴ 要使得f(x)≥0对任意x∈R恒成立,a=1
∴ a的取值集合为{1} 13分
考点:导数,函数的零点,恒成立问题


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
| A、39400 |
| B、-39400 |
| C、78800 |
| D、-78800 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试文科数学试卷(解析版) 题型:选择题
函数f(x)=x+lnx的零点所在的区间为( )
A.(-1,0) B.(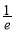 ,1) C.(1,2) D.(1,e)
,1) C.(1,2) D.(1,e)
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试文科数学试卷(解析版) 题型:填空题
定义:如果函数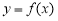 在定义域内给定区间
在定义域内给定区间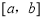 上存在
上存在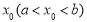 ,满足
,满足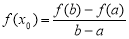 ,则称函数
,则称函数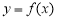 是
是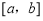 上的“平均值函数”,
上的“平均值函数”,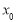 是它的一个均值点.例如
是它的一个均值点.例如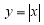 是
是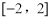 上的平均值函数,0就是它的均值点.若函数
上的平均值函数,0就是它的均值点.若函数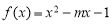 是
是 上的“平均值函数”,则实数m的取值范围是_________.
上的“平均值函数”,则实数m的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试文科数学试卷(解析版) 题型:选择题
已知 是定义在(0,+∞)上的函数,对任意两个不相等的正数x1,x2,都有
是定义在(0,+∞)上的函数,对任意两个不相等的正数x1,x2,都有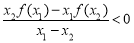 ,记
,记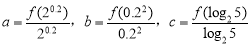 ,则 ( )
,则 ( )
(A)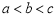 (B)
(B)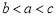
(C)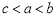 (D)
(D)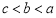
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com