
| A、1 | B、2 | C、3 | D、4 |
| π |
| 2 |


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
| x2 |
| m |
| y2 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:填空题
定义一:对于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2 恒成立,则称函数f(x)在D内有一个宽度为d的.
定义二:若一个函数f(x),对于任意给定的正数?,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为?的,则称f(x)在正无穷处有.下列函数:
①f(x)=lgx,②f(x)=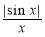 ,③f(x)=-
,③f(x)=-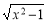 ,④f(x)=
,④f(x)=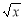 ,⑤f(x)=2x,⑥f(x)=3x-
,⑤f(x)=2x,⑥f(x)=3x-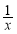
其中在正无穷处有的函数的序号是___________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:解答题
已知向量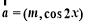 ,
,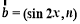 ,函数f(x)=
,函数f(x)=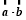 ,且y=f(x)的图象过点
,且y=f(x)的图象过点 和点
和点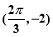 .
.
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com