
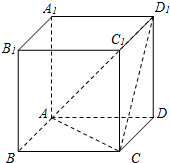
 在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是
在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是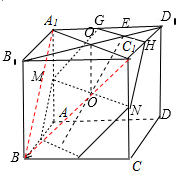 解:截得的三角形中面积最大是以正方体的表面正方形的对角线所构成的等边三角形,如图中的△A1C1B,
解:截得的三角形中面积最大是以正方体的表面正方形的对角线所构成的等边三角形,如图中的△A1C1B,| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
1+
|
| ||
| 2 |
| ||||
| 2 |
| 3 |
| 3 |
| 3 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f(4.5)<f(7)<f(6.5) |
| B、f(7)<f(4.5)<f(6.5) |
| C、f(7)<f(6.5)<f(4.5) |
| D、f(4.5)<f(6.5)<f(7) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com