
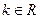 ,函数
,函数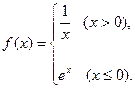 ,
,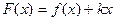 ,
,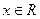 .
.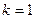 时,求
时,求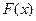 的值域;
的值域;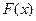 的单调性.
的单调性. ----------1分,
----------1分,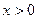 时,
时,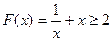 ----------2分;
----------2分;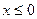 时,
时,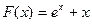 ,根据指数函数与幂函数的单调性,是单调递增函数--------3分,
,根据指数函数与幂函数的单调性,是单调递增函数--------3分, -------4分。所以
-------4分。所以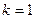 时,
时,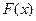 的值域为
的值域为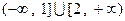 -------5分。
-------5分。 -- ---6分。
-- ---6分。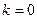 ,当
,当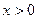 时,
时,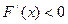 ,
,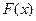 递减,当
递减,当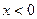 时,
时,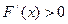 ,
,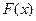 递增 ----8分。
递增 ----8分。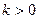 ,当
,当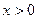 时,解
时,解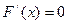 得
得 ,当
,当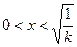 时,
时,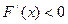 ,
,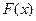 递减,当
递减,当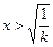 时,
时,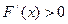 ,
,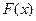 递增。当
递增。当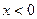 时,
时,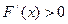 ,
,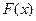 递增-- ---10分。
递增-- ---10分。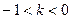 ,当
,当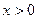 时,
时,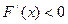 ,
,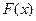 递减。当
递减。当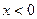 时,解
时,解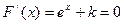 得
得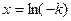 ,当
,当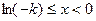 时,
时,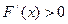 ,
,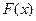 递增,当
递增,当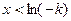 时,
时,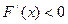 ,
,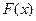 递减-----12分。
递减-----12分。 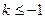 ,对任意
,对任意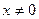 ,
,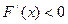 ,
,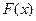 在每个定义域区间上递减--- --13分。
在每个定义域区间上递减--- --13分。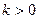 时,
时,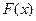 在
在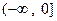 或
或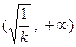 上单调递增,在
上单调递增,在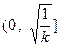 上单调递减;
上单调递减;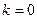 时,
时,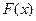 在
在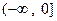 上单调递增,在
上单调递增,在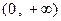 上单调递减;
上单调递减;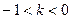 时,
时,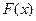 在
在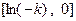 上单调递增,在
上单调递增,在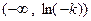 或
或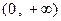 上单调递减;
上单调递减;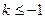 时,
时,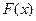 在每个定义域区间上递减---- -14分。
在每个定义域区间上递减---- -14分。

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:不详 题型:解答题
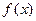 满足下列条件:
满足下列条件: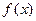 的定义域为[0,1];
的定义域为[0,1];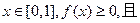
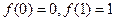 ;
;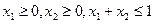 的任意两个数
的任意两个数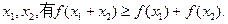
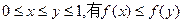 ;
;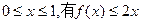 ;
;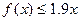 对于一切x∈[0,1]都成立吗?试说明理由.
对于一切x∈[0,1]都成立吗?试说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.[ ,+∞ ,+∞ | B.(1,  | C.[ ,+∞ ,+∞ | D. (1, ] ] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x |
| y |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com