
分析 根据向量的数量积和三角形的面积公式可得tanA=-1,求出A和c的值,再根据余弦定理即可求出a.
解答 解:由$\overrightarrow{AB}•\overrightarrow{AC}$=-6可得bccosA=-6,①,
由三角形的面积公式可得S△ABC=$\frac{1}{2}$bcsinA=3,②
∴tanA=-1,
∵0<A<180°,
∴A=135°,
∴c=$\frac{6}{3×\frac{\sqrt{2}}{2}}$=2$\sqrt{2}$,
由余弦定理可得a2=b2+c2-2bccosA=9+8+12=29
∴a=$\sqrt{29}$
点评 本题考查了向量的数量积公式和三角形的面积公式和余弦定理,考查了学生的运算能力,属于中档题


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与a有关,且与b有关 | B. | 与a有关,但与b无关 | ||
| C. | 与a无关,且与b无关 | D. | 与a无关,但与b有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∩B={x|x<$\frac{3}{2}$} | B. | A∩B=∅ | C. | A∪B={x|x<$\frac{3}{2}$} | D. | AUB=R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
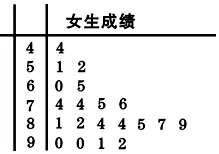 为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).| 优秀 | 非优秀 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
| 参考数据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com