
| A. | $(0,\frac{3}{2})$ | B. | $(0,\frac{{3\sqrt{3}}}{2})$ | C. | $(0,\frac{{\sqrt{3}}}{2})$ | D. | 以上都不对 |
分析 求出函数的导数,得到函数的极值,f(x)=x3-ax2+a(a>0)有且只有一个零点,极小值大于0,列出不等式求解即可.
解答 解:f(x)=x3-ax2+a,(a>0)可得y′=3x2-2ax,令y′=0,可得x=0,或x=$\frac{2a}{3}$,
x<0时y′>0,
x>$\frac{2a}{3}$时,y′>0,
0<x<$\frac{2a}{3}$时,y′<0,
∴函数在(-∞,0),($\frac{2a}{3}$,+∞)单调递增,在(0,$\frac{2a}{3}$)单调递减,
x=0时,函数取的极大值为:a>0.
∴x=$\frac{2a}{3}$时,函数取得极小值:$-\frac{4{a}^{3}}{27}+a$,f(x)=x3-ax2+a(a>0)有且只有一个零点,
必有:$-\frac{4{a}^{3}}{27}+a$>0,解得a∈(0,$\frac{3\sqrt{3}}{2}$),
故选:B.
点评 本题考查了函数的思想,运用求解零点问题,关键构造函数,利用图象交点问题求解,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
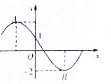 如图所示的函数$f(x)=2sin(wx+φ)(w>0,\frac{π}{2}≤φ≤π)$的部分图象,其中A、B两点之间的距离为5,那么f(-1)=( )
如图所示的函数$f(x)=2sin(wx+φ)(w>0,\frac{π}{2}≤φ≤π)$的部分图象,其中A、B两点之间的距离为5,那么f(-1)=( )| A. | -1 | B. | 2 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-1,∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{3},1)∪(\sqrt{3},+∞)$ | B. | $(-∞,-1)∪(\sqrt{3},+∞)$ | C. | $(-∞,-\sqrt{3})∪(\sqrt{3},+∞)$ | D. | $(-\sqrt{3},-1)∪(1,\sqrt{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com