Question

1．底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的体对角线的长分别是$\sqrt{61}$和$\sqrt{89}$，则这个棱柱的侧面积是100．

Answer 1

分析 根据线面垂直的定义，利用勾股定理求出底面菱形的对角线长，再由菱形的性质算出底面的边长，根据直棱柱的侧面积公式，即可求出该棱柱的侧面积．

解答 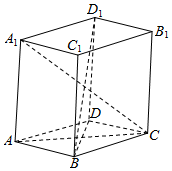解设直四棱柱ABCD-A₁B₁C₁D₁中，对角线A₁C=$\sqrt{61}$，BD₁=$\sqrt{89}$，
∵A₁A⊥平面ABCD，AC?平面ABCD，∴A₁A⊥AC，
Rt△A₁AC中，A₁A=5，可得AC=$\sqrt{{{A}_{1}C}^{2}{{-A}_{1}A}^{2}}$=$\sqrt{{（\sqrt{61}）}^{2}{-5}^{2}}$=6，
同理可得BD=$\sqrt{{{BD}_{1}}^{2}{-{DD}_{1}}^{2}}$=$\sqrt{{（\sqrt{89}）}^{2}{-5}^{2}}$=8；
∵四边形ABCD为菱形，可得AC、BD互相垂直平分，
∴AB=$\sqrt{{（\frac{6}{2}）}^{2}{+（\frac{8}{2}）}^{2}}$=5，即菱形ABCD的边长等于5；
因此，这个棱柱的侧面积为S_侧=（AB+BC+CD+DA）×A₁A=4×5×5=100．
故答案为：100．

点评 本题考查了求直棱柱的侧面积的应用问题，也考查了线面垂直的定义、菱形的性质和直棱柱的侧面积公式等知识，是基础题．