Question

9．如图1，在直角梯形ABCD中，AD∥BC，∠BAD=$\frac{π}{2}$，AB=BC=$\frac{1}{2}$AD=a，E是AD的中点，O是AC与BE的交点，将△ABE沿BE折起到图2中△A₁BE的位置，得到四棱锥A₁-BCDE．
（Ⅰ）证明：CD⊥平面A₁OC；
（Ⅱ）当平面A₁BE⊥平面BCDE时，四棱锥A₁-BCDE的体积为36$\sqrt{2}$，求点E到平面A₁CD的距离h的值．

Answer 1

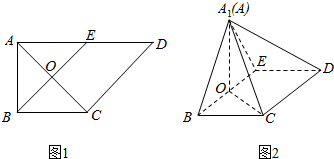
分析 （I）在图1中证明AC⊥BE，则在图2中BE⊥平面A₁OC，再使用平行四边形性质证明CD∥BE即可；
（II）根据棱锥的体积求出a，由BE∥CD即可知道E到平面A₁CD的距离即为O到平面A₁CD的距离，结合（1）的结论即知h也是O到A₁C的距离．

解答 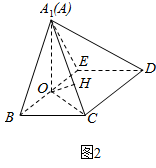解：（Ⅰ）在图1中，因为AB=BC=$\frac{1}{2}AD$=a，E是AD的中点，∠BAD=$\frac{π}{2}$，所以BE⊥AC，
即在图2中，BE⊥A₁O，BE⊥OC，从而BE⊥平面A₁OC．
又CD∥BE，所以CD⊥平面A₁OC．
（Ⅱ）由已知，平面A₁BE⊥平面BCDE，且平面A₁BE∩平面BCDE=BE，
又由（Ⅰ）知，A₁O⊥BE，所以A₁O⊥平面BCDE，
即A₁O是四棱锥A₁-BCDE的高，
由图1可知，A₁O=$\frac{\sqrt{2}}{2}AB=\frac{\sqrt{2}}{2}a$，平行四边形BCDE面积S=BC•AB=a²，
从而四棱锥A₁-BCDE的体积=$\frac{1}{3}×S×{A}_{1}O$=$\frac{1}{3}×{a}^{2}×\frac{\sqrt{2}}{2}a$=$\frac{\sqrt{2}}{6}{a}^{3}$=36$\sqrt{2}$．
解得a=6．
∵BE∥CD，∴点E到平面A₁CD的距离等于点O到平面A₁CD的距离，
由（Ⅰ）知CD⊥平面A₁OC．CD?平面A₁CD，
∴平面A₁OC⊥平面A₁CD，
过O作OH⊥A₁C交A₁C于H，则OH⊥平面A₁CD，
∴点O到平面A₁CD的距离为OH，
在Rt△A₁OC中，A₁O=OC=$\frac{\sqrt{2}}{2}a=3\sqrt{2}$，∴A₁C=6，
∴OH=$\frac{1}{2}$A₁C=3，
∴h=OH=3．

点评 本题考查了面面垂直的性质，线面垂直的判定，棱锥的体积计算，属于中档题．