
设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.记bn= ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.
(1) 若c=0,且b1,b2,b4成等比数列,证明:Sn k=n2Sk(k,n∈N*);
(2) 若{bn}是等差数列,证明:c=0.
证明:∵ {an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和,
∴ Sn=na+ d.
d.
(1) ∵ c=0,∴ bn=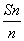 =a+
=a+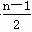 d.
d.
∵ b1,b2,b4成等比数列,∴ b =b1b4,
=b1b4,
∴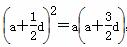
∴  ad-
ad-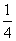 d2=0,
d2=0,
∴ 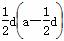 =0.
=0.
∵ d≠0,∴ a= d,∴ d=2a,
d,∴ d=2a,
∴ Sn=na+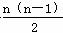 d=na+
d=na+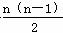 2a=n2a,
2a=n2a,
∴ 左边=Snk=(nk)2a=n2k2a,右边=n2Sk=n2k2a,
∴ 左边=右边,∴ 原式成立.
(2) ∵ {bn}是等差数列,
∴ 设公差为d1,
∴ bn=b1+(n-1)d1
代入bn=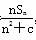 ,得b1+(n-1)d1=
,得b1+(n-1)d1=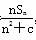 ,
,
∴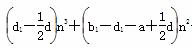 +cd1n=c(d1-b1)对n∈N*恒成立,
+cd1n=c(d1-b1)对n∈N*恒成立,
∴ 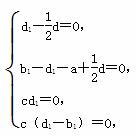
∴ d1= d.∵ d≠0,∴ d1≠0.
d.∵ d≠0,∴ d1≠0.


科目:高中数学 来源: 题型:
已知各项均为正数的数列{an}的前n项的乘积Tn= (n∈N*),bn=log2 an,则数列{bn}的前n项和Sn取最大时,n=________.
(n∈N*),bn=log2 an,则数列{bn}的前n项和Sn取最大时,n=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某科研单位欲拿出一定的经费奖励科研人员,第1名得全部资金的一半多一万元,第2名得剩下的一半多一万元,以名次类推都得到剩下的一半多一万元,到第10名恰好资金分完,则此科研单位共拿出________万元资金进行奖励.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,若a=1,b=2,cosC=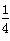 .求:
.求:
(1) △ABC的周长;
(2) cos(A-C)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com