
 在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.
在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.分析 (1)先证明CD⊥平面PAD,再证明平面PAD⊥平面PDC;
(2)根据条件得到棱锥P-BCD的体积最大时的等价条件,建立坐标系,求出平面的法向量,利用向量法进行求解即可.
解答 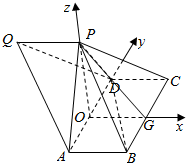 (1)证明:∵侧面ABCD为矩形,∴CD⊥AD,
(1)证明:∵侧面ABCD为矩形,∴CD⊥AD,
∵PA⊥CD,PA∩AD=A,
∴CD⊥平面PAD,
∵CD?平面PDC,
∴平面PAD⊥平面PDC;
(2)过P作AD的垂线,垂足为O,过O作BC垂线,垂足为G,
连接PG,由(1)知,CD⊥平面PAD,
∴CD⊥PO,
∵PO⊥AD,CD∩AD=D,
∴PO⊥平面ABCD,∴PO⊥BC,
∵OG⊥BC,PO∩OG=O,
∴BC⊥平面POG,故BC⊥PG,
在△PBC中,BC=$\sqrt{6}$,PB=$\sqrt{2}$,PC=2,∴BP⊥PC,
∴PG=$\frac{2\sqrt{3}}{3}$,GC=$\frac{2\sqrt{6}}{3}$,BG=$\frac{\sqrt{6}}{3}$,设AB=x,
则OP=$\sqrt{P{G}^{2}-O{G}^{2}}$=$\sqrt{\frac{4}{3}-{x}^{2}}$,
故三棱锥P-BCD的体积S△PBC=$\frac{1}{2}×2×\sqrt{2}$=$\sqrt{2}$,
三棱锥P-BCD的体积VP-BCD=$\frac{1}{3}$×$\frac{1}{2}×\sqrt{6}x×\sqrt{\frac{4}{3}-{x}^{2}}$=$\frac{x\sqrt{8-6{x}^{2}}}{6}$=$\frac{\sqrt{8{x}^{2}-6{x}^{4}}}{6}=\frac{\sqrt{-6({x}^{2}-\frac{2}{3})^{2}+\frac{8}{3}}}{6}$,
∴当x=$\frac{\sqrt{6}}{3}$,即AB=$\frac{\sqrt{6}}{3}$时,三棱锥P-BCD的体积最大,
建立空间直角坐标系如图:则O(0,0,0),B($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$,0),C($\frac{\sqrt{6}}{3}$,$\frac{2\sqrt{6}}{3}$,0),A(0,-$\frac{\sqrt{6}}{3}$,0),
P(0,0,$\frac{\sqrt{6}}{3}$),
故$\overrightarrow{PB}$=($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$),$\overrightarrow{BC}$=(0,$\sqrt{6}$,0),$\overrightarrow{AB}$=($\frac{\sqrt{6}}{3}$,0,0),
设平面BPC的一个法向量为$\overrightarrow{n}$=(x,y,1),则由$\overrightarrow{n}$•$\overrightarrow{PB}$=0,$\overrightarrow{n}$•$\overrightarrow{BC}$=0,
得$\left\{\begin{array}{l}{\frac{\sqrt{6}}{3}x-\frac{\sqrt{6}}{3}y-\frac{\sqrt{6}}{3}=0}\\{\sqrt{6}y=0}\end{array}\right.$得x=1,y=0,即$\overrightarrow{n}$=(1,0,1),
同理得平面APB的一个法向量为$\overrightarrow{m}$=(0,1,-1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-1}{\sqrt{2}•\sqrt{2}}=-$$\frac{1}{2}$,
即<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{2π}{3}$,
即二面角A-BP-C的大小为$\frac{2π}{3}$.
点评 本题考查线面垂直、平面与平面垂直,考查平面与平面的夹角,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力,综合性较强,运算量较大.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
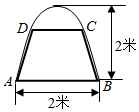 如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.
如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | n<2016? | B. | n≤2016? | C. | n>2016? | D. | n≥2016? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com