
| A. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|>a+b | B. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|≤a+b | C. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|≥a+b | D. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|<a+b |
分析 由集合A可知,$|\overrightarrow{m}|≤1$,从而有$|\overrightarrow{{m}_{1}}|≤1,|\overrightarrow{{m}_{2}}|≤1$,这样便可得到$\overrightarrow{{m}_{1}}•\overrightarrow{{m}_{2}}≤1$,进行数量积的运算便可比较$|a\overrightarrow{{m}_{1}}+b\overrightarrow{{m}_{2}}{|}^{2}$与(a+b)2的关系,从而便可得出$|a\overrightarrow{{m}_{1}}+b\overrightarrow{{m}_{2}}|$与a+b的关系.
解答 解:据题意知,$|\overrightarrow{{m}_{1}}|≤1,|\overrightarrow{{m}_{2}}|≤1$;
∴$\overrightarrow{{m}_{1}}•\overrightarrow{{m}_{2}}=|\overrightarrow{{m}_{1}}||\overrightarrow{{m}_{2}}|cos<\overrightarrow{{m}_{1}},\overrightarrow{{m}_{2}}>≤1$;
∴${a}^{2}{\overrightarrow{{m}_{1}}}^{2}≤{a}^{2},2ab\overrightarrow{{m}_{1}}•\overrightarrow{{m}_{2}}≤2ab$,${b}^{2}{\overrightarrow{{m}_{2}}}^{2}≤{b}^{2}$;
∴${a}^{2}{\overrightarrow{{m}_{1}}}^{2}+2ab\overrightarrow{{m}_{1}}•\overrightarrow{{m}_{2}}+{b}^{2}{\overrightarrow{{m}_{2}}}^{2}$≤a2+2ab+b2;
即$(a\overrightarrow{{m}_{1}}+b\overrightarrow{{m}_{2}})^{2}≤(a+b)^{2}$,a,b≥0;
∴$|a\overrightarrow{{m}_{1}}+b\overrightarrow{{m}_{2}}|≤a+b$.
故选:B.
点评 考查描述法表示集合,根据向量的坐标求向量的长度,以及向量数量积的运算及其计算公式,不等式的性质,要比较$|a\overrightarrow{{m}_{1}}+b\overrightarrow{{m}_{2}}|$与a+b的关系,而去比较$(a\overrightarrow{{m}_{1}}+b\overrightarrow{{m}_{2}})^{2}$与(a+b)2的关系的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>a>c | C. | c>b>a | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
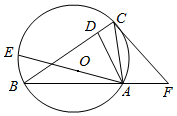 如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.
如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com