
分析 (1)f$′(x)=\frac{1}{x}-ax+1$=-$\frac{a{x}^{2}-x-1}{x}$.分①a≤0,②a>0,讨论单调性;
(2)由(1)得当a≤0时,f(x)在(0,+∞)单调递增,故函数f(x)无极值;当a>0时,f(x)有极大值,其值为f(x2)=lnx2-$\frac{1}{2}a{{x}_{2}}^{2}+{x}_{2}$=lnx2+$\frac{{x}_{2}-1}{2}$.设函数h(x)=lnx+$\frac{x-1}{2}$(x>0),可得$h(x)=lnx+\frac{x-1}{2}$在(0,+∞)上为增函数.可得f(x2)=lnx2+$\frac{{x}_{2}-1}{2}$>0等价于x2>1.即在a>0时,方程ax2-x-1=0的大根大于1,设φ(x)=ax2-x-1,只需φ(1)<0,即a-1-1<0,解得a;
(3)函数y=$\frac{{x}^{3}}{4e}-\frac{1}{2}{x}^{2}+mx-lnx$有零点,则方程$\frac{{x}^{3}}{4e}-\frac{1}{2}{x}^{2}+mx-lnx$=0有实根,即方程$\frac{{x}^{2}}{4e}-\frac{1}{2}x+m-\frac{lnx}{x}=0$有实根,令${y}_{1}=\frac{{x}^{2}}{4e}-\frac{1}{2}x+m$,${y}_{2}=\frac{lnx}{x}$利用两函数单调性在同一坐标系中画出其草图,结合图象可得m的取值范围
解答 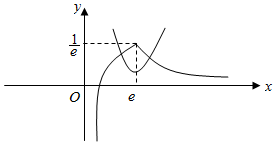 解:(1)函数的定义域为(0,+∞).f$′(x)=\frac{1}{x}-ax+1$=-$\frac{a{x}^{2}-x-1}{x}$.
解:(1)函数的定义域为(0,+∞).f$′(x)=\frac{1}{x}-ax+1$=-$\frac{a{x}^{2}-x-1}{x}$.
①当a≤0时,∵$\frac{1}{x}>0$,-ax>0,∴f′(x)>0,f(x)在(0,+∞)单调递增.
②当a>0时,则△>0,方程ax2-x-1=0的两个实根分别为${x}_{1}=\frac{1-\sqrt{1+4a}}{2a}$<0,${x}_{2}=\frac{1+\sqrt{1+4a}}{2a}$>0.
此时,当x∈(0,x2)时,f′(x)>0,当x∈(x2,+∞)时,f′(x)<0.
∴函数f(x)的单调递增区间为(0,x2),单调递减区间为(x2,+∞).
综上所述,当a>0时,函数f(x)的单调递增区间为(0,$\frac{1+\sqrt{1+4a}}{2a}$),单调递减区间为($\frac{1+\sqrt{1+4a}}{2a}$,+∞).
当a≤0时,f(x)单调递增区间为(0,+∞),无单调递减区间.
(2)解:由(1)得当a≤0时,f(x)在(0,+∞)单调递增,故函数f(x)无极值;
当a>0时,函数f(x)的单调递增区间为(0,$\frac{1+\sqrt{1+4a}}{2a}$),单调递减区间为($\frac{1+\sqrt{1+4a}}{2a}$,+∞).
则f(x)有极大值,其值为f(x2)=lnx2-$\frac{1}{2}a{{x}_{2}}^{2}+{x}_{2}$,∵而$a{{x}_{2}}^{2}-{x}_{2}-1=0$,∴f(x2)=lnx2+$\frac{{x}_{2}-1}{2}$.
设函数h(x)=lnx+$\frac{x-1}{2}$(x>0),则h′(x)=$\frac{1}{x}+\frac{1}{2}>0$,则$h(x)=lnx+\frac{x-1}{2}$在(0,+∞)上为增函数.又h(1)=0,则h(x)>0等价于x>1.
∴f(x2)=lnx2+$\frac{{x}_{2}-1}{2}$>0等价于x2>1.
即在a>0时,方程ax2-x-1=0的大根大于1,设φ(x)=ax2-x-1,
由于φ(x)的图象是开口向上的抛物线,且经过点(0,-1),对称轴x=$\frac{1}{2a}>0$,
则只需φ(1)<0,即a-1-1<0,解得a<2,而a>0,故实数a的取值范围为(0,2).
(3)函数y=$\frac{{x}^{3}}{4e}-\frac{1}{2}{x}^{2}+mx-lnx$有零点,则方程$\frac{{x}^{3}}{4e}-\frac{1}{2}{x}^{2}+mx-lnx$=0有实根,
即方程$\frac{{x}^{2}}{4e}-\frac{1}{2}x+m-\frac{lnx}{x}=0$有实根,
令${y}_{1}=\frac{{x}^{2}}{4e}-\frac{1}{2}x+m$,${y}_{2}=\frac{lnx}{x}$
∵x∈(0,e)时,y1递减,x∈(e,+∞)时,y1递增,
∵x∈(0,e)时,y2递增,x∈(e,+∞)时,y2递减.,
在同一坐标系中其草图如下:
要使函数y=g(x)+mx-lnx有零点,则必须$\frac{{e}^{2}}{4e}-\frac{1}{2}e+m≤\frac{1}{e}$,⇒m≤$\frac{1}{e}+\frac{e}{4}$
∴m的取值范围为(-∞,$\frac{1}{e}+\frac{e}{4}$)
点评 本题考查了导数的综合应用,考查了分类讨论思想、数形结合思想、转化思想,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{11}$ | B. | $\frac{5}{11}$ | C. | $\frac{3}{11}$ | D. | $\frac{2}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
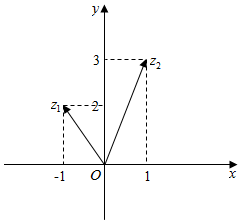 如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2
如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com