练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．圆${C_1}：{x^2}+{y^2}=9$和圆${C_2}：{x^2}+{y^2}-8x+6y+9=0$的位置关系是（　　）
    A．相离B．相交C．内切D．外切

    分析 求出两圆的圆心坐标和半径大小，利用两点的距离公式算出两个圆心之间的距离，再比较圆心距与两圆的半径之和、半径之差的大小关系，可得两圆的位置关系．

    解答 解：∵圆x2+y2-8x+6y+9=0的标准方程为（x-4）2+（y+3）2=16，
    ∴圆x2+y2-8x+6y+9=0的圆心是C2（4，-3），半径=4．
    又∵圆x2+y2=9的圆心是C1（0，0），半径r2=3．
    ∴|C1C2|=5，
    ∵|r1-r2|=1，r1+r2=7，
    ∴|r1-r2|＜|OC|＜r1+r2，可得两圆相交．
    故选B．

    点评 本题给出两圆的方程，判断两圆的位置关系．着重考查了圆的标准方程和圆圆与圆的位置关系等知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知函数$f（x）=\frac{1}{3}{x^3}-\frac{3}{2}{x^2}+2x+5$．
    （1）求函数f（x）的图象在点（3，f（3））处的切线方程．
    （2）若曲线y=f（x）与y=2x+m有三个不同的交点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知全集U=R，函数y=$\sqrt{-{x}^{2}+2x+8}$的定义域为集合A，函数y=$\frac{（x-1）^{0}}{\sqrt{3-x}}$的定义域为集合B．
    （1）求集合A和集合B；
    （2）求A∪B，A∩（∁UB）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知命题p：?x∈R，x-2＞log2x，命题q：?x∈R，x2＞0，则（　　）
    A．p∨q是假命题B．p∨（￢q）是假命题C．p∧q是真命题D．p∧（￢q）是真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．下列说法正确的是（　　）
    A．命题“?x∈R，使得x2＞2x”的否定是“?x∈R，使得x2≤2x”
    B．“若a∈（0，1），则关于x的不等式ax2+2ax+1＞0的解集为R”的逆命题为真
    C．“若a、b不都是偶数，则a+b不是偶数”的否命题为假
    D．“已知a，b∈R若a+b≠3，则a≠2或b≠1”的逆否命题为真

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．与圆${C_1}：{x^2}+{y^2}-4x-10y+13=0$和圆${C_2}：{x^2}+{y^2}+2x+6y+9=0$都相切的直线共有（　　）
    A．1条B．2条C．3条D．4条

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

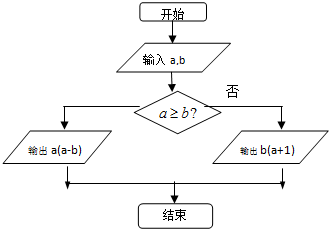
    17．对任意实数若a?b的运算规则如图所示，则$（2cos\frac{5π}{3}）?（lo{g_2}4）$的值为（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．抛物线y2=12x上一点M到抛物线焦点的距离为9，则点M到x轴的距离为6$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设D为△ABC的边AB上一点，P为△ABC内一点，且满足$\overrightarrow{AD}$=$\frac{λ+1}{{λ}^{2}+2}$$\overrightarrow{AB}$，$\overrightarrow{AP}$=$\overrightarrow{AD}$+$\frac{λ}{λ+1}$$\overrightarrow{BC}$，λ＞0，则$\frac{{S}_{△APD}}{{S}_{△ABC}}$的最大值为（　　）
    A．2$\sqrt{2}$B．$\sqrt{2}$C．$\frac{\sqrt{2}}{2}$D．$\frac{\sqrt{2}}{4}$

    查看答案和解析>>

    同步练习册答案