
分析 (1)设送报人到达的时间为X,小王离家去工作的时间为Y,记小王离家前不能看到报纸为事件M;则(X,Y)可以看成平面中的整点,试验的全部结果整点共有3×3=9个,事件M所构成的整点有3个,根据古典概型的计算公式,计算可得答案.
(2)根据题意,设送报人到达的时间为X,小王离家去工作的时间为Y;则(X,Y)可以看成平面中的点,分析可得由试验的全部结果所构成的区域并求出其面积,同理可得事件M所构成的区域及其面积,由几何概型公式,计算可得答案.
解答 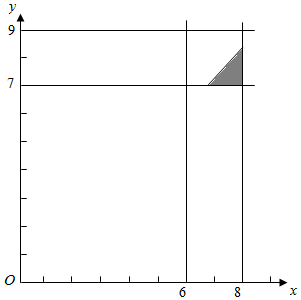 解:(1)设送报人到达的时间为X,小王离家去工作的时间为Y,记小王离家前不能看到报纸为事件M;
解:(1)设送报人到达的时间为X,小王离家去工作的时间为Y,记小王离家前不能看到报纸为事件M;
则(X,Y)可以看成平面中的整点,试验的全部结果所构成的区域为Ω={(X,Y)|6≤X≤8,7≤Y≤9},
整点共有3×3=9个,事件M所构成的区域为A={(X,Y)|6≤X≤8,7≤Y≤9,X≥Y}整点有3个.
是一个古典几何概型,所以P(M)=$\frac{3}{9}=\frac{1}{3}$
(2)如图,设送报人到达的时间为X,小王离家去工作的时间为Y,记小王离家前不能看到报纸为事件M;
则(X,Y)可以看成平面中的点,试验的全部结果所构成的区域为Ω={(X,Y)|6≤X≤8,7≤Y≤9}一个正方形区域,面积为SΩ=4,
事件M所构成的区域为A={(X,Y)|6≤X≤8,7≤Y≤9,X≥Y}即图中的阴影部分,面积为SA=0.5.
这是一个几何概型,所以P(M)=$\frac{{s}_{A}}{{s}_{Ω}}$=$\frac{0.5}{4}=\frac{1}{8}$.
点评 本题考查了古典概型、几何概型的计算公式,属于中档题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
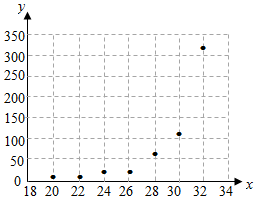 为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并做出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈现线性相关关系,现分别用模型①$y={C_1}{x^2}+{C_2}$与模型;②$y={e^{{C_3}x+{C_4}}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系.
为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并做出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈现线性相关关系,现分别用模型①$y={C_1}{x^2}+{C_2}$与模型;②$y={e^{{C_3}x+{C_4}}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系.| 温度x/°C | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| 产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline x$ | $\overline t$ | $\overline y$ | $\overline z$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{{\sum_{i=1}^7{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({x_i}-\overline x)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({t_i}-\overline t)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({z_i}-\overline z)({x_i}-\overline x)}}}{{\sum_{i=1}^7{{{({x_i}-\overline x)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({z_i}-\overline z)({t_i}-\overline t)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≠$\frac{π}{4}$} | B. | {x|x≠$\frac{π}{4}$,k∈Z} | C. | {x|x≠kπ+$\frac{π}{4}$,k∈Z} | D. | {x|x≠$\frac{3π}{4}$+kπ,k∈Z} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com