Question

13．有下列命题：
①等比数列{a_n}中，前n项和为S_n，公比为q，则S_n，S_2n-S_n，S_3n-S_2n仍然是等比数列，其公比为qⁿ；
②一个正方体的顶点都在球面上，它的棱长为2cm，则球的体积是$4\sqrt{3}π$cm³；
③若数列{a_n}是正项数列，
且$\sqrt{a_1}+\sqrt{a_2}+…+\sqrt{a_n}={n^2}+3n（n∈{N^*}）$，
则$\frac{a_1}{2}+\frac{a_2}{3}+…+\frac{a_n}{n+1}=2{n^2}+6n$；
④在△ABC中，∠BAC=120°，AB=2，AC=1，D是边BC上的一点（包括端点），则${\overrightarrow{AD}^{\;}}{•^{\;}}\overrightarrow{BC}$的取值范围是[-5，2]．
其中正确命题的序号是②③④（填番号）

Answer 1

分析 ①考虑公比为q，若q=-1，且n为偶数，则S_n=0，S_2n-S_n=0，S_3n-S_2n=0，即可判断；
②考虑正方体的对角线即为球的直径，求得半径，再由球的条件计算即可判断；
③求出n=1时的首项，将n换为n-1，可得通项公式，再由等差数列的求和公式，计算即可判断；
④由数量积的定义可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=2×1×cos120°=-1．再由向量的加减运算和数量积的性质，平面向量基本定理，计算即可得到所求范围，即可判断．

解答 解：①等比数列{a_n}中，前n项和为S_n，公比为q，若q=-1，且n为偶数，
则S_n=0，S_2n-S_n=0，S_3n-S_2n=0，不为等比数列，故①错；
②一个正方体的顶点都在球面上，它的棱长为2cm，则球的直径为2r=2$\sqrt{3}$，即r=$\sqrt{3}$，
可得体积是$\frac{4}{3}$π×（$\sqrt{3}$）³=$4\sqrt{3}π$cm³，故②正确；
③若数列{a_n}是正项数列，且$\sqrt{a_1}+\sqrt{a_2}+…+\sqrt{a_n}={n^2}+3n（n∈{N^*}）$，
则$\sqrt{{a}_{1}}$=4，可得a₁=16，当n≥2时，$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n-1}}$=（n-1）²+（n-1），
相减可得$\sqrt{{a}_{n}}$=2n+2，即有a_n=4（n+1）²，对n=1也成立，
可得$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{3}$+…+$\frac{{a}_{n}}{n+1}$=8+12+…+4（n+1）=4×$\frac{1}{2}$n（2+n+1）=2n²+6n，故③正确；
④∵D是边BC上的一点（包括端点），
∴可设$\overrightarrow{AD}$=λ$\overrightarrow{AB}$+（1-λ）$\overrightarrow{AC}$（0≤λ≤1）．
∵∠BAC=120°，AB=2，AC=1，
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=2×1×cos120°=-1．
∴$\overrightarrow{AD}$•$\overrightarrow{BC}$=[λ$\overrightarrow{AB}$+（1-λ）$\overrightarrow{AC}$]•（$\overrightarrow{AC}$-$\overrightarrow{AB}$）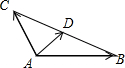
=（2λ-1）$\overrightarrow{AB}$•$\overrightarrow{AC}$-λ$\overrightarrow{AB}$²+（1-λ）$\overrightarrow{AC}$²=-（2λ-1）-4λ+1-λ=-7λ+2．
∵0≤λ≤1，∴（-7λ+2）∈[-5，2]．
∴$\overrightarrow{AD}$•$\overrightarrow{BC}$的取值范围是[-5，2]．故④正确．
故答案为：②③④

点评 本题考查命题的真假判断，主要是等比数列求和的性质、正方体的外接球的性质和数列的通项公式的求法和求和，以及向量数量积的性质和运用，考查推理和运算能力，属于中档题．