
分析 (1)利用对数函数的定义域以及三角函数线求解即可.
(2)利用对数运算法则以及二倍角公式化简求解即可.
解答 解:(1)函数f(x)=lg(2sin2x-1)有意义,
可得2sin2x-1>0,即sin2x>$\frac{1}{2}$.可得2k$π+\frac{π}{6}$<2x<2kπ+$\frac{5π}{6}$,k∈Z,
解得k$π+\frac{π}{12}$<x<kπ+$\frac{5π}{12}$,k∈Z,
函数的定义域为:{x|k$π+\frac{π}{12}$<x<kπ+$\frac{5π}{12}$,k∈Z}.
(2):${log_2}cos\frac{π}{9}+{log_2}cos\frac{2π}{9}+{log_2}cos\frac{4π}{9}$=$lo{g}_{2}(cos\frac{π}{9}cos\frac{2π}{9}cos\frac{4π}{9})$=log2($\frac{8sin\frac{π}{9}cos\frac{π}{9}cos\frac{2π}{9}cos\frac{4π}{9}}{8sin\frac{π}{9}}$)
=$lo{g}_{2}(\frac{sin\frac{8π}{9}}{8sin\frac{π}{9}})$=-3.
点评 本题考查三角函数的定义域,三角函数线,二倍角公式的应用,对数运算法则的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | cos(x+$\frac{3π}{16}$) | B. | cos(4x+$\frac{3π}{16}$) | C. | cos4x | D. | cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $5\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0≤k≤3 | B. | k≥3 | C. | k≤0或k≥3 | D. | k≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-3,1,\sqrt{6}})$和$({3,-1,-\sqrt{6}})$ | B. | $({-\frac{3}{4},\frac{1}{4},\frac{{\sqrt{6}}}{4}})$ | ||
| C. | $({-\frac{3}{4},\frac{1}{4},\frac{{\sqrt{6}}}{4}})$和$({\frac{3}{4},-\frac{1}{4},-\frac{{\sqrt{6}}}{4}})$ | D. | $({3,-1,-\sqrt{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
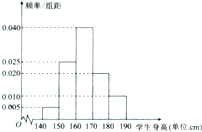 从某校高三的1000名学生中用随机抽样的方法,得到其中100人的身高数据(单位:cm,所得数据均在[140,190]上),并制成频率分布直方图(如图所示),由该图可估计该校高三学生中身高不低于165cm的人数约为( )
从某校高三的1000名学生中用随机抽样的方法,得到其中100人的身高数据(单位:cm,所得数据均在[140,190]上),并制成频率分布直方图(如图所示),由该图可估计该校高三学生中身高不低于165cm的人数约为( )| A. | 500 | B. | 550 | C. | 600 | D. | 700 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={(\frac{1}{2})^x}$ | B. | y=cosx | C. | y=ln|x| | D. | y=1-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com