
| A. | $\frac{9}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{9}$ |
分析 写出展开式的通项,利用展开式中x4的系数为70,$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$,即可求出a的值.
解答 解:二项式(a+$\frac{x}{b}$)7(其中$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$)的展开式的通项为Tr+1=${C}_{7}^{r}•{a}^{7-r}•{b}^{-r}•{x}^{r}$,
∵展开式中x4的系数为70,
∴${C}_{7}^{4}•{a}^{3}•{b}^{-4}$=70,
∵$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$,
∴a=$\frac{2}{9}$,
故选:D.
点评 本题考查二项式定理,考查学生的计算能力,确定展开式的通项是关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:解答题
 为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆O及等腰直角三角形EFH,其中FE⊥FH.为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边EH上,且AD∥BC∥HF,设∠AOE=θ.
为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆O及等腰直角三角形EFH,其中FE⊥FH.为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边EH上,且AD∥BC∥HF,设∠AOE=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 24种 | C. | 36种 | D. | 72种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
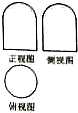 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )| A. | 5π | B. | 6π | C. | 7π | D. | 9π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com