
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
分析 根据平面向量数量积的定义与投影的定义,进行计算即可.
解答 解:∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=5,
∴(2$\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=2${\overrightarrow{a}}^{2}$-$\overrightarrow{b}$•$\overrightarrow{a}$=2×22-5×2×cos60°=3,
∴向量2$\overrightarrow{a}$-$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•(2\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}|}$=$\frac{3}{2}$.
故选:A.
点评 本题考查了平面向量数量积的定义与投影的计算问题,是基础题目.


 同步轻松练习系列答案
同步轻松练习系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2}^{8}eln2}$ | B. | $\frac{1}{{2}^{9}}$ | C. | $\frac{e}{{2}^{8}ln2}$ | D. | $\frac{e}{{2}^{9}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
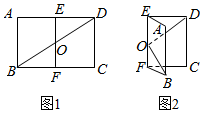 如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:
如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
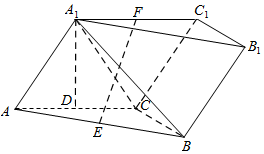 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | $({\frac{{2\sqrt{3}}}{3},2})$ | C. | $(1,\sqrt{3})$ | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com