
在 中,已知
中,已知 .
.
(1)求证: ;
;
(2)若 求角A的大小.
求角A的大小.
(1)证明见解析;(2) .
.
解析试题分析:(1)已知的向量的数量积,要证明的是角的关系,故我们首先运用数量积定义把已知转化为三角形的边角关系,由已知可得 ,即
,即 ,考虑到求证式只是角的关系,因此我们再应用正弦定理把式子中边的关系转化为角的关系,即有
,考虑到求证式只是角的关系,因此我们再应用正弦定理把式子中边的关系转化为角的关系,即有 ,而这时两边同除以
,而这时两边同除以 即得待证式(要说明
即得待证式(要说明 均不为零).(2)要求解
均不为零).(2)要求解 的大小,一般是求出这个角的某个三角函数值,本题应该求
的大小,一般是求出这个角的某个三角函数值,本题应该求 ,因为(1)中有
,因为(1)中有 可利用,思路是
可利用,思路是 .
.
试题解析:(1)∵ ,∴
,∴ ,
,
即 . 2分
. 2分
由正弦定理,得 ,∴
,∴ . 4分
. 4分
又∵ ,∴
,∴ .∴
.∴ 即
即 . 6分
. 6分
(2)∵ ,∴
,∴ .∴
.∴ .8分
.8分
∴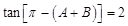 ,即
,即 .∴
.∴ . 10分
. 10分
由 (1) ,得 ,解得
,解得 . 12分
. 12分
∵ ,∴
,∴ .∴
.∴ . 14分
. 14分
考点:(1)向量的数量积的定义与正弦定理;(2)已知三角函数值,求角.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com