
在平面直角坐标系中,已知向量a=(x,y- ),b=(kx,y+
),b=(kx,y+ )(k∈R),a⊥b,动点M(x,y)的轨迹为T.
)(k∈R),a⊥b,动点M(x,y)的轨迹为T.
(1 )求轨迹T的方程,并说明该方程表示的曲线的形状.
)求轨迹T的方程,并说明该方程表示的曲线的形状.
(2)当k=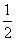 时,已知点B(0,-
时,已知点B(0,- ),是否存在直线l:y=x+m ,使点B关于直线l的对称点落在轨迹T上?若存在,求出直线l的方程;若不存在,请说明理由.
),是否存在直线l:y=x+m ,使点B关于直线l的对称点落在轨迹T上?若存在,求出直线l的方程;若不存在,请说明理由.
解析:(1)∵a⊥b,∴ a·b=(x,y- )·(kx,y+
)·(kx,y+ )=0,得kx2+y2-2=0,即kx2+y2=2.
)=0,得kx2+y2-2=0,即kx2+y2=2.
当k=0时,方程表示两条与x轴平行的直线;
当k=1时,方程表示以原点为圆心,以 为半径的圆;
为半径的圆;
当k>0且k≠1时,方程表示椭圆;
当k<0时,方程表示焦点在y轴上的 双曲线.
双曲线.
(2)当k=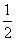 时,动点M的轨迹T的方程为
时,动点M的轨迹T的方程为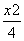 +
+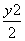 =1,
=1,
设满足条件的直线l存在,点B关于直线l的对称点为B′(x0,y0),则由BB′⊥l得,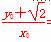 =-1,由BB′的中点在l上得
=-1,由BB′的中点在l上得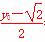 =
=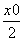 +m,解得x0=-
+m,解得x0=- -m,y0=m.
-m,y0=m.
∵点B′(x0,y0)在椭圆上,∴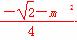 +
+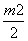 =1.整理得3m2+2
=1.整理得3m2+2 m-2=0,解得m=
m-2=0,解得m=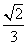 或m=-
或m=- .
.
∴直线l的方程为y=x+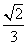 或y=x-
或y=x- .
.
经检验y=x+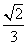 和y=x-
和y=x- 都符合题设.∴满足条件的直线l存在,其方程为y=x+
都符合题设.∴满足条件的直线l存在,其方程为y=x+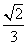 或y=x-
或y=x- .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,设抛物 线y2=4x的焦点为F,准线为l,P为抛物线上一点,
线y2=4x的焦点为F,准线为l,P为抛物线上一点, PA⊥l,A为垂足.如果直线AF的倾斜角为120°,那么|PF|=____________.
PA⊥l,A为垂足.如果直线AF的倾斜角为120°,那么|PF|=____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为( )
A.x2 -
-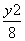 =1(x>1) B.x2-
=1(x>1) B.x2-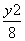 =1(x<-1)
=1(x<-1)
C.x2+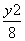 =1(x>0) D.x2-
=1(x>0) D.x2-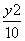 =1(x>1)
=1(x>1)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:“∀x∈[0,1],a≤ex”,命题q:“∃x∈R,x2-4x+a=0”,若命题p,q均是真命题,则实数a的取值范围是( )
A.[4,+∞) B.[1,4]
C.[e,4] D.(-∞,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,
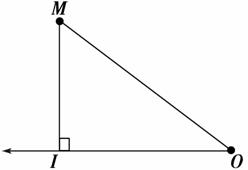
一辆汽车从O点出发沿一条直线公路以50公里/小时的速度匀速行驶(图中的箭头方向为汽车行驶方向),汽车开动的同时,在距汽车出发点O点的距离为5公里,距离公路线的垂直距离为3公里的M点的地方有一个人骑摩托车出发想把一件东西送给汽车司机.问骑摩托车的人至少以多大的速度匀速行驶才能实现他的愿望,此时他驾驶摩托车行驶了多少公里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com