
(本题满分12分)已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0,②f(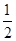 )=1,③对任意x,y
)=1,③对任意x,y ( 0,+∞),
( 0,+∞),
都有f(xy)= f(x)+ f(y),求不等式f(x)+ f(5-x)≥-2的解集。
 。
。
解析试题分析:(1)构造函数中两个任意变量的函数值差,结合函数表达式得到函数单调性的证明。
(2)结合特殊值的函数值,得到f(4)=-2,进而得到函数的不等式的求解。
解:设0<x1<x2,则 >1,∵f(xy)= f(x)+ f(y)
>1,∵f(xy)= f(x)+ f(y)
∴f(x2)= f(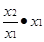 )= f(
)= f( )+ f(x1)
)+ f(x1)
又∵x>1时,f(x)<0,∴f( )<0
)<0
∴f(x2)<f(x1),∴f(x)是( 0,+∞)上的减函数。又∵f(1)= f(1)+ f(1)
∴f(1)=0,而f(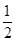 )=1,∴f(2?
)=1,∴f(2?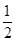 )= f(2)+ f(
)= f(2)+ f(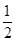 )=0
)=0
∴f(2)=-1,∴f(x)+ f(5-x)≥-2="2" f(2)= f(4)
∴ ,∴0<x≤1,或4≤x<5
,∴0<x≤1,或4≤x<5
∴原不等式的解集是 。
。
考点:本题主要考查了函数的单调性的运用。
点评:解决该试题的关键是能利用已知条件分析得到函数的单调性的证明,结合已知的关系式将所求的表示为一个整体函数式,同时能结合单调性得到求解。


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
(10分)设 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)证明 在区间
在区间 内单调递增;
内单调递增;
(3)若对于区间[3,4]上的每一个 的值,不等式
的值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知平面上的线段l及点P,在l上任取一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作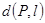 。
。
(1)已知点 ,线段
,线段 ,求
,求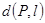 ;
;
(2)设A(-1,0),B(1,0),求点集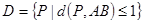 所表示图形的面积;
所表示图形的面积;
(3)若M(0,1),O(0,0),N(2,0),画出集合 所表示的图形。(本题满分14分)
所表示的图形。(本题满分14分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com