
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 根据抛物线的方程求出准线方程是x=-2,结合抛物线的定义可得|AF|=x1+2且|BF|=x2+2,两式相加并结合x1+x2=5,即可得到|AB|的值为9.
解答 解:∵抛物线方程为y2=8x,
∴p=4,可得抛物线的准线方程是x=-2,
∵过抛物线 y2=8x的焦点F作直线交抛物线于A(x1,y1)B(x2,y2),
∴根据抛物线的定义,可得|AF|=x1+$\frac{p}{2}$=x1+2,|BF|=x2+$\frac{p}{2}$=x2+2,
因此,线段AB的长|AB|=|AF|+|BF|=x1+x2+4,
又∵x1+x2=5,∴|AB|=x1+x2+4=9.
故选D.
点评 本题给出抛物线焦点弦AB端点A、B的横坐标的关系式,求AB的长度,着重考查了抛物线的定义、标准方程和简单几何性质等知识,属于中档题.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
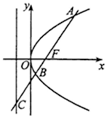 如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )| A. | y2=3x | B. | y2=9x | C. | y2=$\frac{3}{2}$x | D. | y2=$\frac{9}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
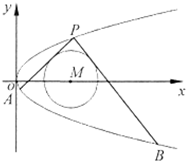 已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.
已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com