
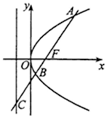
 如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )| A. | y2=3x | B. | y2=9x | C. | y2=$\frac{3}{2}$x | D. | y2=$\frac{9}{2}$x |
分析 根据过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,作AM、BN垂直准线于点M、N,根据|BC|=2|BF|,且|AF|=3,和抛物线的定义,可得∠NCB=30°,设A(x1,y1),B(x2,y2),|BF|=x,而x1+$\frac{p}{2}$=3,x2+$\frac{p}{2}$=1,且x1x2=$\frac{{p}^{2}}{4}$,即有(3-$\frac{p}{2}$)(1-$\frac{p}{2}$)=$\frac{{p}^{2}}{4}$,可求得p的值,即求得抛物线的方程.
解答  解:设A(x1,y1),B(x2,y2),
解:设A(x1,y1),B(x2,y2),
作AM、BN垂直准线于点M、N,则|BN|=|BF|,
又|BC|=2|BF|,得|BC|=2|BN|,
∴∠NCB=30°,
有|AC|=2|AM|=6,
设|BF|=x,则2x+x+3=6⇒x=1,
而x1+$\frac{p}{2}$=3,x2+$\frac{p}{2}$=1,且x1x2=$\frac{{p}^{2}}{4}$,
∴(3-$\frac{p}{2}$)(1-$\frac{p}{2}$)=$\frac{{p}^{2}}{4}$,解得p=$\frac{3}{2}$.
得y2=3x.
故选A.
点评 此题是个中档题.考查抛物线的定义以及待定系数法求抛物线的标准方程.体现了数形结合的思想,特别是解析几何,一定注意对几何图形的研究,以便简化计算.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | (2,1) | C. | (1,2) | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-$\frac{1}{8}$ | B. | x=$\frac{1}{8}$ | C. | y=-$\frac{1}{8}$ | D. | y=$\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com