
分析 若“p∨(¬q)”为真命题,“(¬p)∨q”也为真命题,则p为真命题,则q也为真命题;若p为假命题,则q也为假命题,进而可得a的取值范围.
解答 解:(Ⅰ)若p为真命题,
则f′(x)=x2-2x+5-a2≥0恒成立,
则△=4-4(5-a2)≤0,
解得:-2≤a≤2.
g′(x)=$\frac{{(x-1){e^x}}}{x^2}$,故g(x)=$\frac{e^x}{x}$在[1,+∞)上递增,
若q为真命题,
则a≥1.
由已知可得若p为真命题,则q也为真命题;
若p为假命题,则q也为假命题,
当p,q同真时,1≤a≤2;
同假时,a<-2,
故a∈(-∞,-2)∪[1,2].(12分)
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的单调性,利用导数研究函数的单调性等知识点,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
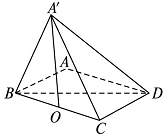 如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.
如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com