
分析 求导函数,可得函数的单调性,进而可求函数的最值,即可得到结论.
解答 解:∵y=$\frac{1}{100}$(x3+4x+16),
∴y′=$\frac{1}{100}(3{x}^{2}+4)$>0,
∴函数y=$\frac{1}{100}$(x3+4x+16)是增函数,满足条件①.
设g(x)=$\frac{y}{x}$=$\frac{1}{100}$(${x}^{2}+4+\frac{16}{x}$),
则g′(x)=$\frac{(x-2)({x}^{2}+2x+4)}{50{x}^{2}}$,
令g′(x)=0,得x=2.
当x<2时,g′(x)<0,g(x)在(-∞,2)上是减函数;
当x>2时,g′(x)>0,g(x)在(2,+∞)上是增函数,
又a=1,b=4,即x∈[1,2],g(x)在[1,2]上是减函数,在[1,4]上是增函数,
∴当x=2时,g(x)有最小值=16%>15%,
当x=4时,g(x)=24%<25%,x=1时,g(x)=25%≤25%.
∴能采用函数模型y=$\frac{1}{100}$(x3+4x+16)作为生态环境改造投资方案.
点评 本题考查利用数学知识解决实际问题,考查导数知识的运用,考查学生分析解决问题的能力,正确求导是关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
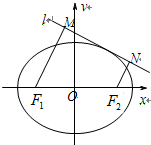 已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.
已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 0 | D. | -$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由金、银、铜、铁可导电,猜想:金属都可以导电 | |
| B. | 猜想数列5,7,9,11,…的通项公式为an=2n+3 | |
| C. | 由正三角形的性质得出正四面体的性质 | |
| D. | 半径为r的圆的面积S=π•r2,则单位圆的面积S=π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{8}$,$\frac{1}{4}$) | B. | ($\frac{1}{12}$,$\frac{1}{4}$) | C. | ($\frac{1}{12}$,$\frac{1}{8}$) | D. | ($\frac{1}{8}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com