
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 患色盲 | 不患色盲 | 总计 | |
| 女性 | 6 | 514 | 520 |
| 男性 | 38 | 442 | 480 |
| 总计 | 44 | 956 | 1000 |
| 1000×(442×6-38×514)2 |
| 44×956×480×520 |


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
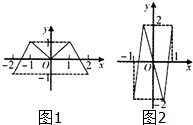 如图,偶函数f(x)的图象形如字母M(图1),奇函数g(x)的图象形如字母N(图2),若方程f(g(x))=0.g(f(x))=0的实根个数分别为a,b,则a+b=( )
如图,偶函数f(x)的图象形如字母M(图1),奇函数g(x)的图象形如字母N(图2),若方程f(g(x))=0.g(f(x))=0的实根个数分别为a,b,则a+b=( )| A、18 | B、21 | C、24 | D、27 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、两条对角线相等的四边形是矩形 |
| B、矩形的两条对角线不相等 |
| C、有的矩形两条对角线不相等 |
| D、对角线不相等的四边形不是矩形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| π |
| 2 |
| 3π |
| 2 |
| a |
| b |
| 8 |
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| a |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com