练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    观察下列问题：
    已知（1-2x）2013=a0+a1x+a2x2+a3x3+…+a2013x2013，
    令x=1，可得a0+a1+a2+…+a2013=（1-2•1）2013=-1，
    令x=1，可得a0-a1+a2+…-a2013=（1+2•1）2013=32013，
    请仿照这种“赋值法”，令x=0，得到a0=
     
    ，并求出
    a1
    2
    +
    a2
    22
    +
    a3
    23
    +…+
    a2013
    22013
    =
     
    ．
    考点：归纳推理
    专题：推理和证明
    分析：仿照这种“赋值法”，令x=0，可得a0=1，再令x=0，可得a0=1，从而求得出
    a1
    2
    +
    a2
    22
    +
    a3
    23
    +…+
    a2013
    22013
    ．
    解答： 解：∵已知（1-2x）2013=a0+a1x+a2x2+a3x3+…+a2013x2013
    令x=0，可得a0=（1-0）2013=0，
    再令x=0，可得a0=1，
    则
    a1
    2
    +
    a2
    22
    +
    a3
    23
    +…+
    a2013
    22013
    =0-1=-1，
    故答案为：1，-1
    点评：本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设a＞b＞c＞1，记M=a-
    		c
    ，N=a-
    		b
    ，P=2（
    a+b
    2
    -
    		ab
    ），Q=3（
    a+b+c
    3
    -
    3abc
    ），试找出中的最小者，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下表中的数阵为“森德拉姆数筛”，其特点是每行每列都成等差数列，记第i行第j列的数为aij，则数字73在表中出现的次数为
     
    ．
     2 3 4 5 6 7…
     3 5 7 9 11 13…
     4 7 10 13 16 19…
     5 9 13 17 21 25…
     6 11 16 21 26 31…
     7 13 19 25 31 37…
    …………………

    查看答案和解析>>

    科目：高中数学 来源： 题型：

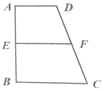    如图梯形ABCD中，AD∥BC，∠ABC=90°，AD：BC：AB=2：3：4，E、F分别是AB，CD的中点，将四边形ADFE沿直线EF进行翻折．给出四个结论：
    ①DF⊥BC，
    ②BD⊥FC
    ③平面DBF⊥平面BFC，
    ④平面DCF⊥平面BFC．
    在翻折过程中，可能成立的结论是
     
    ．（填写结论序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若P为曲线
    x=secα
    y=tanα
    （α为参数）上的动点，O为坐标原点，M为线段OP的中点，则点M的轨迹方程是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

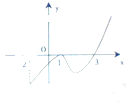    如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
    ①3是函数y=f（x）的极大值点；
    ②1是函数y=f（x）的极值点；
    ③当x＞3时，f（x）＞0恒成立；
    ④函数y=f（x）在x=-2处切线的斜率小于零；
    ⑤函数y=f（x）在区间（-2，3）上单调递减．
    则正确命题的序号是
     
    （写出所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）=
    1
    x
    -1，x≥1
    lnx，0＜x＜1
    ，若函数g（x）=f（x）-kx+k只有一个零点，则k的取值范围是（　　）
    A、（-∞，-1）∪（1，+∞）
    B、（-1，1）
    C、[0，1]
    D、（-∞，-1]∪[0，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a＞0，设p：存在a∈R，使y=ax是R上的单调递减函数； q：存在a∈R，使函数g（x）=lg（2ax2+2x+1）的值域为R，如果“p∧q”为假，“p∨q”为真，则a的取值范围是（　　）
    A、（
    1
    2
    ，1）
    B、（
    1
    2
    ，+∞）
    C、（0，
    1
    2
    ]∪[1，+∞）
    D、（0，
    1
    2
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1-2x）7=a0+a1x+a2x2+…+a7x7，则a1+a2+…+a7=
     
    ．

    查看答案和解析>>

    同步练习册答案