练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．命题“?x0∈（0，+∞），ln x0=x0-1”的否定是（　　）
    A．?x∈（0，+∞），ln x≠x-1B．?x∉（0，+∞），ln x=x-1
    C．?x0∈（0，+∞），ln x0≠x0-1D．?x0∉（0，+∞），ln x0=x0-1

    分析 利用特称命题的否定是全称命题，写出结果即可．

    解答 解：因为特称命题的否定是全称命题，所以，命题“?x0∈（0，+∞），ln x0=x0-1”的否定是：?x∈（0，+∞），ln x≠x-1．
    故选：A．

    点评 本题考查特称命题与全称命题的否定关系，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．2016年1月2日凌晨某公司公布的元旦全天交易数据显示，天猫元旦当天全天的成交金额为315.5亿元．为了了解网购者一次性购物情况，某统计部门随机抽查了1月1日100名网购者的网购情况，得到如表数据统计表，已知网购金额在2000元以上（不含2000元）的频率为0.4．
    网购金额（元）频数频率
    （0，500]50.05
    （500，1000]xp
    （1000，1500]150.15
    （1500，2000]250.25
    （2000，2500]300.3
    （2500，3000]yq
    合计1001.00
    （1）先求出x，y，p，q的值，再将如图3所示的频率分布直方图绘制完整；
    （2）对这100名网购者进一步调查显示：购物金额在2000元以上的购物者中网龄3年以上的有35人，购物金额在2000元以下（含2000元）的购物者中网龄不足3年的有20人，请填写下面的列联表，并据此判断能否在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关？
    x网龄3年以上网龄不足3年合计
    购物金额在2000元以上35
    购物金额在2000元以下20
    总计100
    参考数据：
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
    （3）从这100名网购者中根据购物金额分层抽出20人给予返券奖励，为进一步激发购物热情，在（2000，2500]和（2500，3000]两组所抽出的8人中再随机抽取2人各奖励1000元现金，求（2000，2500]组获得现金将的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．直线l：y=x+1上的点到圆C：x2+y2+2x+4y+4=0上的点的最近距离为（　　）
    A．$\sqrt{2}$B．2-$\sqrt{2}$C．1D．$\sqrt{2}$-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．命题“若a+b+c=3，则a2+b2+c2≥3”的逆命题是（　　）
    A．“若a2+b2+c2≥3，则a+b+c=3”B．“若a2+b2+c2＜3，则a+b+c≠3”
    C．“若a2+b2+c2≥3，则a+b+c≠3”D．“若a2+b2+c2＜3，则a+b+c=3”

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．计算：sin（-$\frac{π}{4}$）=-$\frac{\sqrt{2}}{2}$，cos（-$\frac{π}{6}$）=$\frac{\sqrt{3}}{2}$，tan（-$\frac{7π}{6}$）=$-\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．求适合下列条件的双曲线的标准方程
    （Ⅰ）过点（3，-1），且离心率$e=\sqrt{2}$；
    （Ⅱ）一条渐近线为$y=-\frac{3}{2}x$，顶点间距离为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+4x，x≥0}\\{4x-{x}^{2}，x＜0}\end{array}\right.$，若f（3-2a）＞f（a），则实数a的取值范围是（-∞，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

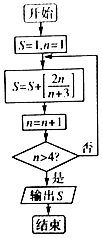    12．若[x]表示不超过x的最大整数，如[2，6]=2，[-2，6]=-3，执行如图所示的程序框图，记输出的值为S0，则${log_{\frac{1}{3}}}{S_0}$=（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知函数f（x）是定义在R上的奇函数，且x≤0时f（x）=3x-2x+m（m∈R，m为常数），则f（2）=$-\frac{28}{9}$．

    查看答案和解析>>

    同步练习册答案