
分析 作出图形,使用余弦定理求出台风中心距A300千米时的时间,则两根之差为台风持续时间.
解答 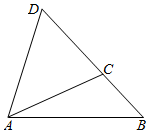 解:设t小时后A地会受到台风影响,台风中心为C,则BC=40t,
解:设t小时后A地会受到台风影响,台风中心为C,则BC=40t,
在△ABC中,AB=400,AC=300,BC=40t,B=45°,
由余弦定理得cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{70000+1600{t}^{2}}{32000t}$=$\frac{\sqrt{2}}{2}$,
解得t1=5$\sqrt{2}-$$\frac{5}{2}$,t2=5$\sqrt{2}$$+\frac{5}{2}$,
∴t2-t1=5.
∴问从现在起5$\sqrt{2}$-$\frac{5}{2}$小时后气象台A会受到台风影响,持续影响的时间为5小时.
点评 本题考查了解三角形的实际应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{4}$] | C. | (0,$\frac{π}{3}$] | D. | (0,$\frac{π}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(tan($\frac{1}{2}π-1$))>f(cot1) | B. | f(cos$\frac{5}{6}π$)$<f(cos\frac{π}{3})$ | C. | f(sin2)>f(cos2) | D. | f(cos1)>f(sin1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com