
分析 (I)通过设数列{an}的首项为a1,公差为d(≠0),代入计算即得an=3n-4;当n=1时由4S1=b12+2b1-3可知b1=3,当n≥2时,利用4Sn=bn2+2bn-3与4Sn-1=bn-12+2bn-1-3作差,整理可知数列{bn}是首项为3、公差为2的等差数列,进而可知bn=2n+1;
(Ⅱ)通过(I)裂项可知cn=$\frac{1}{6}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),并项相加可知Tn=$\frac{n}{3(2n+1)}$,进而可知$\frac{{T}_{n}}{{T}_{n+1}}$=1-$\frac{1}{2{n}^{2}+3n+1}$,通过令f(x)=1-$\frac{1}{2{x}^{2}+3x+1}$,借助函数知识可知$\frac{{T}_{n}}{{T}_{n+1}}$≥$\frac{5}{6}$,从而问题转化为解不等式$\frac{{a}_{m}}{{a}_{m+1}}$≤$\frac{5}{6}$,计算即得结论.
解答 解:(I)设数列{an}的首项为a1,公差为d(≠0),
由已知可得$\left\{\begin{array}{l}{{a}_{1}+2d=5}\\{({a}_{1}+3d)^{2}=({a}_{1}+d)({a}_{1}+11d)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{a}_{1}=-1}\\{d=3}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=5}\\{d=0}\end{array}\right.$(舍),
∴an=3n-4;
当n=1时,4S1=b12+2b1-3,解得:b1=3或b1=-1(舍),
当n≥2时,4Sn-1=bn-12+2bn-1-3,
∴4bn=4Sn-4Sn-1=bn2+2bn-bn-12-2bn-1,
整理得:(bn-bn-2-2)(bn+bn-2)=0,
又∵数列{bn}的每一项均为正实数,
∴bn-bn-2-2=0,
∴数列{bn}是首项为3、公差为2的等差数列,
∴bn=2n+1;
(Ⅱ)由(I)可知cn=$\frac{1}{(2{a}_{n}+5){b}_{n}}$=$\frac{1}{(6n-3)(2n+1)}$=$\frac{1}{6}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
则Tn=$\frac{1}{6}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{6}$(1-$\frac{1}{2n+1}$)=$\frac{n}{3(2n+1)}$,
∴$\frac{{T}_{n}}{{T}_{n+1}}$=$\frac{n(2n+3)}{(n+1)(2n+1)}$=1-$\frac{1}{2{n}^{2}+3n+1}$,
令f(x)=1-$\frac{1}{2{x}^{2}+3x+1}$,则当x>0时,f(x)>0,
∴{$\frac{{T}_{n}}{{T}_{n+1}}$}为递增数列,$\frac{{T}_{n}}{{T}_{n+1}}$≥$\frac{{T}_{1}}{{T}_{2}}$=$\frac{5}{6}$,
又∵$\frac{{T}_{n}}{{T}_{n+1}}$≥$\frac{{a}_{m}}{{a}_{m+1}}$ 对?n∈N* 恒成立,
∴$\frac{{a}_{m}}{{a}_{m+1}}$=$\frac{3m-4}{3m-1}$≤$\frac{5}{6}$,
解得:m≤$\frac{19}{3}$,
故正整数m的最大值为6.
点评 本题考查数列的通项及前n项和,考查裂项相消法,考查数列的单调性,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若m,n是异面直线,则α与β相交 | B. | 若m∥β,n∥α则α∥β | ||
| C. | 若m⊥n,则α⊥β | D. | 若m⊥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | [0,1) | C. | [0,1] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<0} | B. | {x|0<x≤2} | C. | {x|0<x<2} | D. | {x|0<x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
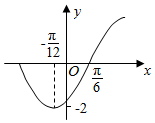
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | 7 | C. | -$\frac{1}{7}$ | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-2) | B. | (-2,0) | C. | (-$\frac{5}{2}$,1) | D. | (-3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com