考点:归纳推理
专题:规律型
分析:左边是连续奇数的和,右边是相应奇数个数的立方,关键是求出第n个等式中的首项奇数,可得答案.
解答:
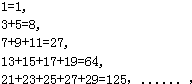
解:由题意,左边是连续奇数的和,右边是相应奇数个数的立方,
由第1个式子的第一个奇数为1=12-1+1,最后一个奇数为1=12+1-1,
由第2个式子的第一个奇数为3=22-2+1,最后一个奇数为5=22+2-1,
由第3个式子的第一个奇数为7=32-3+1,最后一个奇数为11=32+3-1,
由第4个式子的第一个奇数为13=42-4+1,最后一个奇数为19=42+4-1,
由第5个式子的第一个奇数为21=52-5+1,最后一个奇数为29=52+5-1,
…
可得:第n个等式中的首项奇数:n2-n+1,最后一个奇数为n2+n-1,
∴所以第n个等式应为:(n2-n+1)+(n2-n+3)+(n2+n+5)+…+(n2+n+1)=n3,
故答案为:(n2-n+1)+(n2-n+3)+(n2+n+5)+…+(n2+n+1)=n3
点评:本题主要考查归纳推理,关键是分析第n个等式中的首项奇数,从而寻找规律,得出结论.