练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    曲线f（x）=2x在x=0处的切线方程为（　　）
    A、y=x-1
    B、y=x+1
    C、y=（x-1）ln2
    D、y=xln2+1
    考点：利用导数研究曲线上某点切线方程
    专题：导数的综合应用
    分析：求出f（0）的值，得到切点坐标，再求出f′（0），即切线的斜率，然后直接由直线方程的斜截式得切线方程．
    解答： 解：由f（x）=2x，得f（0）=1，
    ∴切点坐标为（0，1）．
    又f′（x）=2xln2，
    ∴f′（0）=20•ln2=ln2，
    则曲线f（x）=2x在x=0处的切线方程为y=xln2+1．
    故选：D．
    点评：本题考查利用导数研究曲线上某点处的切线方程，过曲线上某点处的切线的斜率，就是该点处的导数值，是中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    袋中装有3个红球和2个黑球，一次取3个球．
    （Ⅰ）求取出的3个球中有2个红球的概率；
    （Ⅱ）取出的3个球中，红球数多于黑球数的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过点P（2，3）且与直线2x+y-1=0垂直的直线方程是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在命题“若x2-7x+6=0，则x=1”的逆命题、否命题、逆否命题中，真命题的个数为（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    曲线f（x）=x3+2x-1在点P0处的切线平行于直线y=5x+2，则点P0坐标为（　　）
    A、（1，2）
    B、（-1，-4）
    C、（1，2）或（-1，-4）
    D、（2，4）或（-1，-4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设P和Q是两个集合，定义集合P-Q={x|x∈P且x∉Q}，如果P={x|log2x＜1}，Q={x|1＜x＜3}，那么P-Q等于（　　）
    A、{x|0＜x＜1}
    B、{x|0＜x≤1}
    C、{x|1≤x＜2}
    D、{x|2≤x＜3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设等差数列{an}的前n项和为Sn，已知（a2012-1）3+2014a2012=0，（a3-1）3+2014a3=4028，则下列结论正确的是（　　）
    A、S2014=2014，a2012＜a3
    B、S2014=2014，a2012＞a3
    C、S2014=2013，a2012＜a3
    D、S2014=2013，a2012＞a3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinα-2cosα=0，计算：
    （1）
    sinα-2cosα
    5cosα-sinα
    ；
    （2）
    1
    2sinαcosα+cos2α
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

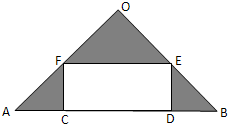    为响应党的十八大提出的文化强国建设的号召，某县政府计划建立一个文化产业园区，计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅，如图点C、D在底边AB上，E、F分别在腰OB、OA上，已知OA=OB=30米，AB=30
    		2
    米，OE=x米，x∈[14，20]．
    （1）试用x表示S，并求S的取值范围；
    （2）若矩形CDEF展厅的每平方米造价为
    37k
    		S
    ，绿化（图中阴影部分）的每平方米造价为
    12k
    		S
    （k为正常数），求总造价W关于S的函数W=f（S），并求当OE为何值时总造价W最低．

    查看答案和解析>>

    同步练习册答案