
���� ��1�����������ƽ����ϵ�������C1����ͨ���̣��ɦ�2=x2+y2���������C2��ֱ�����귽�̣�
��2���������C2�������̣���P��IJ������꣬�����M��N�����꣬���������ľ��빫ʽ���|PM|+|PN|�������ٻ���|PM|+|PN|��2���������Һ�������ֵ�����|PM|+|PN|��2����ֵ���������|PM|+|PN|�����ֵ��
��� �⣺��1������C1�IJ�������Ϊ$\left\{{\begin{array}{l}{x=2cos��}\\{y=\sqrt{3}sin��}\end{array}}\right.$���ɵ����ߵ�ֱ������ķ���Ϊ$\frac{x^2}{4}+\frac{y^2}{3}=1$��
����C2�ķ��̱�Ϊ$\left\{{\begin{array}{l}{x'=cos��}\\{y'=cos��}\end{array}}\right.$������C2��ֱ������ķ���Ϊx2+y2=1��
��$\left\{{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}}\right.$�������������ߵķ��̿ɵ�3��2cos2��+4��2sin2��=12��
������C1�ķ���Ϊ3��2+��2sin2��=12������C2�ļ�����ķ���Ϊ��=1��
��2������C1�ķ���Ϊ$\frac{x^2}{4}+\frac{y^2}{3}=1$���������Ҷ���ֱ�Ϊ��-2��0������2��0��������C2�ķ���Ϊx2+y2=1�����P��cos����sin������$|{PM}|+|{PN}|=\sqrt{{{��cos��+2��}^2}+{{sin}^2}��}+\sqrt{{{��cos��-2��}^2}+{{sin}^2}��}=\sqrt{5+4cos��}+\sqrt{5-4cos��}$��${��|{PM}|+|{PN}|��^2}=10+2\sqrt{25-16{{cos}^2}��}��10+2\sqrt{25-16��0}=20$��
��${��|{PM}|+|{PN}|��_{max}}=2\sqrt{5}$
��cos��=0ʱ��sin��=��1��
��P������Ϊ��0��1����0��-1��ʱ��ȡ���ֵ��
���� ���⿼��������̡������귽������ͨ���̵�ת���������ľ��빫ʽ���Լ�����ֵ���⣬���黯��������


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
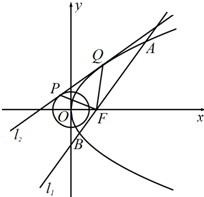 ��ͼ����������C��y2=2px��p��0���Ľ���ΪF������F��ֱ��l1��������C��A��B���㣬��|AB|=8���߶�AB���е㵽y��ľ���Ϊ3��ֱ��l2��Բ${x^2}+{y^2}=\frac{1}{2}$���ڵ�P����������C���ڵ�Q�����FPQ�������������
��ͼ����������C��y2=2px��p��0���Ľ���ΪF������F��ֱ��l1��������C��A��B���㣬��|AB|=8���߶�AB���е㵽y��ľ���Ϊ3��ֱ��l2��Բ${x^2}+{y^2}=\frac{1}{2}$���ڵ�P����������C���ڵ�Q�����FPQ�������������| A�� | $\frac{3}{2}$ | B�� | 2 | C�� | $\frac{{\sqrt{3}}}{4}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
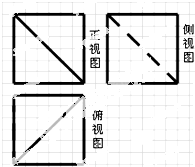 ��ͼ������ֽ��С�����εı߳�Ϊ1������������һ�����屻��ȥһ���ֺ����ü����������ͼ����ü�����ı����Ϊ��������
��ͼ������ֽ��С�����εı߳�Ϊ1������������һ�����屻��ȥһ���ֺ����ü����������ͼ����ü�����ı����Ϊ��������| A�� | 54 | B�� | 162 | C�� | 54+18$\sqrt{3}$ | D�� | 162+18$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
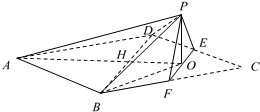 �߳�Ϊ4������ABCD�У������DCB=60�㣬��E��F�ֱ��DZ�CD��CB���е㣬AC��BD�ڵ�H��AC��EF�ڵ�O����EF����CEF���۵���PEF��λ�ã�ʹƽ��PEF��ƽ��ABD������PA��PB��PD���õ���ͼ��ʾ������P-ABFED��
�߳�Ϊ4������ABCD�У������DCB=60�㣬��E��F�ֱ��DZ�CD��CB���е㣬AC��BD�ڵ�H��AC��EF�ڵ�O����EF����CEF���۵���PEF��λ�ã�ʹƽ��PEF��ƽ��ABD������PA��PB��PD���õ���ͼ��ʾ������P-ABFED���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�����ABCD��ֱ�����Σ�AB��AD��AB��CD��$CD=2AB=2BP=\sqrt{2}AD$��$\overrightarrow{CE}=��\overrightarrow{EB}$���ˣ�0����DE��ƽ��PBC������ABP�͵���ABCD
��ͼ��������P-ABCD�У�����ABCD��ֱ�����Σ�AB��AD��AB��CD��$CD=2AB=2BP=\sqrt{2}AD$��$\overrightarrow{CE}=��\overrightarrow{EB}$���ˣ�0����DE��ƽ��PBC������ABP�͵���ABCD�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com