
分析 建立坐标系,设OC=ρ,代入坐标运算即可求出$\frac{λ}{μ}$.
解答 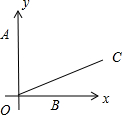 解:∵$\overrightarrow{OA}•\overrightarrow{OB}=0$,∴OA⊥OB,
解:∵$\overrightarrow{OA}•\overrightarrow{OB}=0$,∴OA⊥OB,
以O为原点,以OA,OB为坐标轴建立坐标系,
则A(0,$\sqrt{3}$),B(1,0),设OC=ρ,则C($\frac{\sqrt{3}}{2}ρ$,$\frac{1}{2}ρ$),
∵$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$(λ,μ∈R),
∴$\left\{\begin{array}{l}{μ=\frac{\sqrt{3}}{2}ρ}\\{\sqrt{3}λ=\frac{1}{2}ρ}\end{array}\right.$,∴$\frac{λ}{μ}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了平面向量的基本定理,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
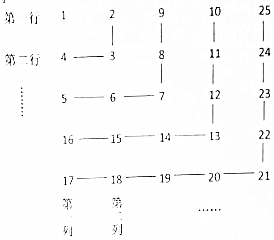
| A. | 20162 | B. | 2016×2017 | C. | 20172 | D. | 2017×2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 48 | B. | 52 | C. | 56 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 按如图程序框图运算:若运算进行3次才停止,则输入的x的取值范围是( )
按如图程序框图运算:若运算进行3次才停止,则输入的x的取值范围是( )| A. | (10,28] | B. | (10,28) | C. | [10,28) | D. | [10,28] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(3)=3 | B. | P(5)=1 | C. | P(2003)>P(2005) | D. | P(2008)<P(2010) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com