考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由线面垂直得D
1D⊥AC,又AC⊥BD,从而AC⊥平面D
1DBB
1,进而AC⊥B
1D,同理可证D
1C⊥B
1D,由此能证明B
1D⊥平面CD
1O,.
(2)由已知得AC⊥DE,要使平面CDE⊥平面CD
1O,只需DE⊥平面CD
1O,即需DE⊥D
1O,设D
1D=2,则DO=
,由此能求出
=2,由|D
1E|=λ|EO|,得λ=2.
解答:
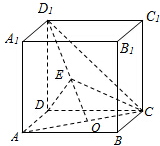
解:(1)证明:∵D
1D⊥平面ABCD,∴D
1D⊥AC,
又AC⊥BD,∴AC⊥平面D
1DBB
1,∴AC⊥B
1D,
同理可证D
1C⊥B
1D,∴B
1D⊥平面CD
1O.
(2)解:∵O为AC的中点,∴在△D
1AC中,D
1O⊥AC,
又∵D
1D⊥AC,∴AC⊥平面D
1OD,∴AC⊥DE,
要使平面CDE⊥平面CD
1O,只需DE⊥平面CD
1O,
即需DE⊥D
1O,(∵PE⊥AC,∴DE⊥平面CD
1O),
设D
1D=2,则DO=
,∴在Rt△D
1DO中,OD
1=
,
∴DE=
=
,
∴
D1E==
,
∴EO=
,∴
=2,∵|D
1E|=λ|EO|,∴λ=2.
点评:本题考查线面垂直的证明,考查使得面面垂直的实数值的求法,考查方程思想、等价转化思想等数学思想方法和学生的空间想象能力、逻辑推理能力和运算求解能力,是中档题.

 如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|.
如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|. 解:(1)证明:∵D1D⊥平面ABCD,∴D1D⊥AC,
解:(1)证明:∵D1D⊥平面ABCD,∴D1D⊥AC,

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案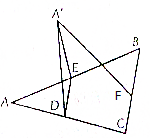 如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?
如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?