Question

17．用斜二测画法画一个周长为4的矩形的直观图，此直观图面积的最大值为（　　）

• A． $2\sqrt{2}$
• B． $\sqrt{2}$
• C． $\frac{{\sqrt{2}}}{2}$
• D． $\frac{{\sqrt{2}}}{4}$

Answer 1

分析 在已知图形所在的空间中取水平平面，作X′轴，Y′轴使∠X′O′Y′=45°，然后依据平行投影的有关性质逐一作图．利用基本不等式求直观图面积的最大值．

解答 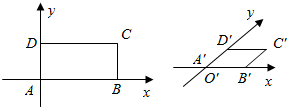解：（1）在已知ABCD中取AB、AD所在边为X轴与Y轴，相交于O点（O与A重合），画对应X′轴，Y′轴使∠X′O′Y′=45°
（2）在X′轴上取A′，B′使A′B′=AB，在Y′轴上取D′，
使A′D′=$\frac{1}{2}$AD，过D′作D′C′平行X′的直线，且等于A′D′长．
（3）连C′B′所得四边形A′B′C′D′就是矩形ABCD的直观图．
设矩形的长、宽分别为a，b，则a+b=2≥2$\sqrt{ab}$，
∴ab≤1，∴直观图面积的最大值为a$•\frac{1}{2}b•\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{4}$．
故选D．

点评 本题考查平面图形的直观图的画法：斜二测画法，考查作图能力，属基础知识的考查．