
分析 由题意将圆C和直线l先化为一般方程坐标,然后再计算曲线C上到直线l距离为$\frac{{7\sqrt{10}}}{10}$的点的个数.
解答 解:化曲线C的参数方程为普通方程:(x-2)2+(y-1)2=9,
圆心(2,1)到直线x-3y+2=0的距离d=$\frac{|2-3+2|}{\sqrt{10}}$=$\frac{1}{\sqrt{10}}$<3,
直线和圆相交,过圆心和l平行的直线和圆的2个交点符合要求,
又$\frac{1}{\sqrt{10}}$+$\frac{{7\sqrt{10}}}{10}$<3
在直线l的另外一侧有圆上的2个点符合要求,
故答案为4
点评 解决这类问题首先把曲线C的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系得出结论.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 不等边锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1,1 | B. | -$\frac{3}{2}$,-1 | C. | -$\frac{3}{2}$,3 | D. | -2,$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
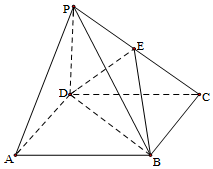 在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1≤b≤2 | B. | b≤-1或b≥2 | C. | -1<b<2 | D. | b<-1或b>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤3} | B. | {x|1≤x≤3} | C. | {x|0≤x≤4} | D. | {x|1<x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com