
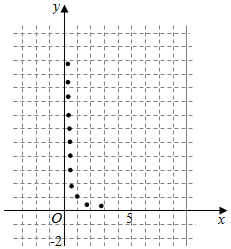
 某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且做了一定的数据处理(如表),做出了散点图(如图).
某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且做了一定的数据处理(如表),做出了散点图(如图).| $\overline x$ | $\overline y$ | $\overline w$ | $\sum_{i=1}^{10}{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^{10}{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^{10}{({x_i}-\overline x)}({y_i}-\overline y)$ | $\sum_{i=1}^{10}{({w_i}-\overline w)}({y_i}-\overline y)$ |
| 1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
分析 (1)根据散点图是否按直线型分布作答;
(2)根据回归系数公式得出y关于ω的线性回归方程,再得出y关于x的回归方程;
(3)利用基本不等式得出煤气用量的最小值及其成立的条件.
解答 解:(1)$y=c+\frac{d}{x^2}$更适宜作烧水时间y关于开关旋转角x的回归方程类型.
(2)由公式可得:$d=\frac{16.2}{0.81}=20,c=20.6-20×0.78=5$,所以回归方程为y=5+$\frac{20}{{x}^{2}}$.
(3)设t=kx,则煤气用量S=yt=kx(5+$\frac{20}{{x}^{2}}$)=5kx+$\frac{20k}{x}$≥2$\sqrt{5kx•\frac{20k}{x}}$=20k,
当且仅当5kx=$\frac{20k}{x}$时取“=”,即x=2时,煤气用量最小.
点评 本题考查了可化为线性相关的回归方程的求解,基本不等式的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一只转盘,均匀标有8个数,现转动转盘,则转盘停止转动时,指针向奇数的概率是( )
如图,一只转盘,均匀标有8个数,现转动转盘,则转盘停止转动时,指针向奇数的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$+…<2 | ||
| C. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1 | D. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
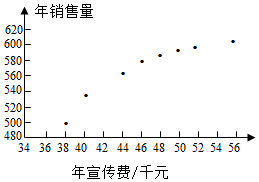 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{n}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{n}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{n}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{n}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [e+1,+∞) | B. | (e+1,+∞) | C. | (e-1,+∞) | D. | [e-1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com