Question

16．已知O，A，B，C，P在同一平面上，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，其中$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$，（$\overrightarrow{c}$-$\overrightarrow{a}$）•（2$\overrightarrow{c}$-$\overrightarrow{b}$）=0，$\overrightarrow{OP}$=$λ\overrightarrow{OA}$+$μ\overrightarrow{OB}$（1≤λ，μ≤2），则|$\overrightarrow{CP}$|的取值范围是$[\frac{\sqrt{19}-\sqrt{3}}{4}，\frac{\sqrt{127}+\sqrt{3}}{4}]$．

Answer 1

分析 根据条件即可求出$∠AOB=\frac{π}{3}$，并可由$（\overrightarrow{c}-\overrightarrow{a}）•（2\overrightarrow{c}-\overrightarrow{b}）=0$得出$（\overrightarrow{c}-\overrightarrow{a}）⊥（\overrightarrow{c}-\frac{1}{2}\overrightarrow{b}）$，可取OB的中点D，并连接AD，从而可以得出点C在以AD为直径的圆上．可延长OA到A′，OB到B′，分别以OA，OB为邻边作平行四边形OAEB，以OA′，OB′为邻边作平行四边形OA′FB′，并延长AE交B′F于H，延长BE交A′F于G，从而平行四边形EHFG及其内部即为点P所在区域，取AD的中点O′，并连接O′E，O′F，可求出O′E，O′F的值，从而可以得出$|\overrightarrow{CP}|$的最小值和最大值，从而得出$|\overrightarrow{CP}|$的取值范围．

解答 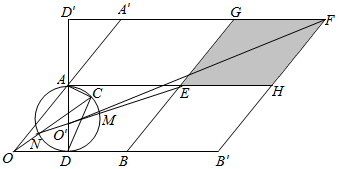解：$|\overrightarrow{a}|=1，|\overrightarrow{b}|=1$，∴$\overrightarrow{a}•\overrightarrow{b}=cos∠AOB=\frac{1}{2}$；
∴$∠AOB=\frac{π}{3}$；
由$（\overrightarrow{c}-\overrightarrow{a}）•（2\overrightarrow{c}-\overrightarrow{b}）=0$得，$（\overrightarrow{c}-\overrightarrow{a}）•（\overrightarrow{c}-\frac{1}{2}\overrightarrow{b}）=0$；
∴$（\overrightarrow{c}-\overrightarrow{a}）⊥（\overrightarrow{c}-\frac{1}{2}\overrightarrow{b}）$；
如图，作$\overrightarrow{OA}=\overrightarrow{a}，\overrightarrow{OB}=\overrightarrow{b}$，$\overrightarrow{OC}=\overrightarrow{c}$，$∠AOB=\frac{π}{3}$，取OB中点D，连接CA，CD，则：$\overrightarrow{c}-\overrightarrow{a}=\overrightarrow{AC}，\overrightarrow{c}-\frac{1}{2}\overrightarrow{b}=\overrightarrow{DC}$；
∴AC⊥DC；
∴C点在以AD为直径的圆上
以OA，OB为邻边作平行四边形OAEB，延长OA到A′，使OA′=2，延长OB到B′，使OB′=2，分别以OA′，OB′为邻边作平行四边形OA′FB′，延长BE交A′F于G，延长AE交B′F于H；
则图中阴影部分便为P点所在区域；
设AD的中点为O′，连接O′E，O′F，延长DA交FA′的延长线于D′；
据题意知，AD⊥OB，且AD=$\frac{\sqrt{3}}{2}$；
∴$O′A=\frac{\sqrt{3}}{4}$，$O′D′=\frac{3\sqrt{3}}{4}$，且AE=1，D′F=$\frac{5}{2}$；
∴$O′E=\sqrt{\frac{3}{16}+1}=\frac{\sqrt{19}}{4}$，$O′F=\sqrt{\frac{27}{16}+\frac{25}{4}}=\frac{\sqrt{127}}{4}$；
∴$|\overrightarrow{CP}|$的最小值为$\frac{\sqrt{19}-\sqrt{3}}{4}$，最大值为$\frac{\sqrt{127}+\sqrt{3}}{4}$；
∴$|\overrightarrow{CP}|$的取值范围为$[\frac{\sqrt{19}-\sqrt{3}}{4}，\frac{\sqrt{127}+\sqrt{3}}{4}]$．
故答案为：[$\frac{\sqrt{19}-\sqrt{3}}{4}，\frac{\sqrt{127}+\sqrt{3}}{4}$]．

点评 考查单位向量的概念，向量数量积的计算公式，已知三角函数值求角，向量的数乘运算，以及向量垂直的充要条件，圆的直径所对的圆周角为直角，向量加法的平行四边形法则，以及直角三角形边的关系，数形结合解题的方法．