
| A. | (-$\frac{1}{32}$,0) | B. | (-$\frac{1}{16}$,0) | C. | (0,$\frac{1}{32}$) | D. | (0,$\frac{1}{16}$) |
分析 根据f(x)的图象判断x2的范围和x1,x2,x3的关系,得出x1x2x3关于x2的函数,利用单调性求出该函数的值域.
解答 解:令g(x)=f(x)-a=0得f(x)=a,
做出f(x)的函数图象如图所示: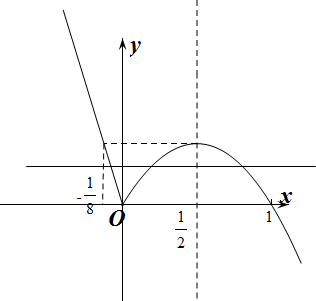
∵g(x)有三个不同的零点x1,x2,x3,
则-$\frac{1}{8}$<x1<0,0<x<$\frac{1}{2}$,x2+x3=1.且-2x1=-x22+x2,
∴x1=$\frac{{{x}_{2}}^{2}-{x}_{2}}{2}$,x3=1-x2.
∴x1x2x3=$\frac{{{x}_{2}}^{2}-{x}_{2}}{2}$•x2•(1-x2)=-$\frac{1}{2}$x24+x23-$\frac{1}{2}$x22,
令h(x2)=-$\frac{1}{2}$x24+x23-$\frac{1}{2}$x22,则h′(x2)=-2x23+3x22-x2=-x2(2x2-1)(x2-1),
∵0<x2<$\frac{1}{2}$,∴h′(x2)<0,
∴h(x2)在(0,$\frac{1}{2}$)上是减函数,
又h(0)=0,h($\frac{1}{2}$)=-$\frac{1}{32}$.
∴-$\frac{1}{32}$<h(x2)<0.
另解:设-2x=a,即x1=-$\frac{1}{2}$a,(0<a<$\frac{1}{4}$),
-x2+x=a,可得x2x3=a,
则x1x2x3=-$\frac{1}{2}$a2∈(-$\frac{1}{32}$,0).
故选A.
点评 本题考查了函数零点与图象的关系,函数值域的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|x<1} | C. | {x|0≤x<1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
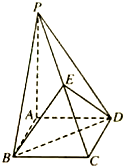 如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.
如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
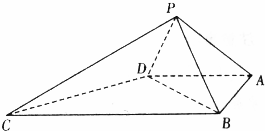 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD=2,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD=2,△PAB与△PAD都是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com