
分析 (1)求出g(x)的最小值,根据最小值大于0,求出b的范围即可;
(2)问题转化为et-lnt≤x3+bx2+3,设h(t)=et-lnt,t∈[1,2],得到h(t)≥e,问题转化为e≤x3+bx2+3对x∈[1,2]恒成立,根据函数的单调性求出b的范围即可.
解答 解:(1)∵g(x)=x+$\frac{2}{x}$+b≥2$\sqrt{2}$+b(x>0),
∴$g{(x)_{min}}=2\sqrt{2}+b$,
∴g(x)在(0,+∞)上没零点
$?g{(x)_{min}}=2\sqrt{2}+b>0$$?b>-2\sqrt{2}$,
∴$b∈(-2\sqrt{2},+∞)$;
(2)∵et-lnt-4≤f(x)-2x
?et-lnt≤x3+bx2+3,
设h(t)=et-lnt,t∈[1,2],
∵h′(t)=e-$\frac{1}{t}$≥0对t∈[1,2]恒成立,
∴h(t)在t∈[1,2]上单调递增,
∴h(t)≥h(1)=e,
∴e≤x3+bx2+3对x∈[1,2]恒成立,
∴$b≥-(x+\frac{3-e}{x^2})$对x∈[1,2]恒成立,
设$m(x)=-(x+\frac{3-e}{x^2})$,x∈[1,2],
∵m′(x)=-1+$\frac{6-2e}{{x}^{3}}$≤5-2e<0,
∴m(x)在x∈[1,2]递减,
∴m(x)≤M(1)=e-4,
∴b≥e-4,即b∈[e-4,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | “若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | “?x∈R,x3-x2+1≤0”的否定是“?x∈R,x3-x2+1>0“ | |
| D. | “△ABC中,若A>B,则sinA>sinB”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③ | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,$\frac{π}{2}$) | B. | (3,-$\frac{π}{2}$) | C. | (3,0) | D. | (3,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
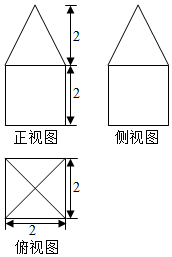
| A. | 8 cm3 | B. | 12 cm3 | C. | $\frac{32}{3}$ cm3 | D. | $\frac{40}{3}$ cm3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com