
分析 (Ⅰ)依题意,$\frac{1}{a^2}+\frac{9}{{4{b^2}}}=1$,$\frac{c}{a}=\frac{1}{2}$,a2=b2+c2,解得a,$b=\sqrt{3}$,c,可得椭圆C的标准方程.
(Ⅱ)依题意,直线PQ过点$({\frac{1}{2},0})$.①当直线PQ的斜率不为0时,可设其方程为$x=my+\frac{1}{2}$,联立$\left\{\begin{array}{l}x=my+\frac{1}{2}\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$消去x得4(3m2+4)y2+12my-45=0,设点P(x1,y1),Q(x2,y2),R(x0,y0),直线AR的斜率为k,利用韦达定理表示斜率.在求范围.②当直线PQ的斜率为0时,线段PQ的中点R与坐标原点重合,AR的斜率为0.
解答 解:(Ⅰ)依题意,$\frac{1}{a^2}+\frac{9}{{4{b^2}}}=1$,$\frac{c}{a}=\frac{1}{2}$,a2=b2+c2,
解得a=2,$b=\sqrt{3}$,c=1,
故椭圆C的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)依题意,直线PQ过点$({\frac{1}{2},0})$.①当直线PQ的斜率不为0时,可设其方程为$x=my+\frac{1}{2}$,
联立$\left\{\begin{array}{l}x=my+\frac{1}{2}\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$消去x得4(3m2+4)y2+12my-45=0,
设点P(x1,y1),Q(x2,y2),R(x0,y0),直线AR的斜率为k,
故${y_1}+{y_2}=-\frac{3m}{{3{m^2}+4}}$,${y_0}=-\frac{3m}{{2({3{m^2}+4})}}$,
当m=0时,k=0,
当m≠0时,$k=\frac{1}{{4m+\frac{4}{m}}}$,因为$|{4m+\frac{4}{m}}|=4|m|$$+\frac{4}{|m|}≥8$,故$0<\frac{1}{{4|m|+\frac{4}{|m|}}}≤\frac{1}{8}$,
当且仅当$4|m|=\frac{4}{|m|}$,即|m|=1时等号成立.
故$0<k≤\frac{1}{8}$,故$\frac{1}{8}≤k≤\frac{1}{8}$且k≠0.
②当直线PQ的斜率为0时,线段PQ的中点R与坐标原点重合,AR的斜率为0.
综上所述,直线AR的斜率的取值范围为$[{-\frac{1}{8},\frac{1}{8}}]$.
点评 本题考查了椭圆的方程,直线与椭圆的位置关系,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 都不大于-2 | B. | 都不小于-2 | ||
| C. | 至少有一个不大于-2 | D. | 至少有一个不小于-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ | B. | $\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | C. | $-\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | D. | $-\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | (?p)∨q | D. | (?p)∧(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
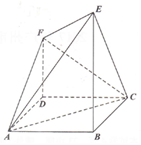 如图,ABCD是边长为a的正方形,EB⊥平面ABCD,FD⊥平面ABCD,$EB=2FD=\sqrt{2}a$.
如图,ABCD是边长为a的正方形,EB⊥平面ABCD,FD⊥平面ABCD,$EB=2FD=\sqrt{2}a$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
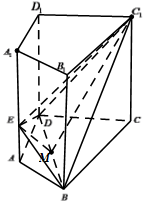 如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.
如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com