
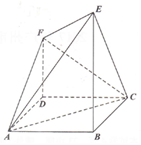
 如图,ABCD是边长为a的正方形,EB⊥平面ABCD,FD⊥平面ABCD,$EB=2FD=\sqrt{2}a$.
如图,ABCD是边长为a的正方形,EB⊥平面ABCD,FD⊥平面ABCD,$EB=2FD=\sqrt{2}a$.分析 (Ⅰ)连接BD,推导出AC⊥BD,AC⊥FD,从而AC⊥平面BDF.推导出EB∥FD,从而B,D,F,E四点共面,由此能证明EF⊥AC.
(Ⅱ)设AC∩BD=O,连接EO,FO,由VE-FAC=VA-FEO+VC-FEO,能求出三棱锥E-FAC的体积.
解答 证明::(Ⅰ)连接BD,因为ABCD是正方形,所以AC⊥BD.
因为FD⊥平面ABCD,AC?平面ABCD,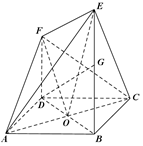 所以AC⊥FD.
所以AC⊥FD.
因为BD∩FD=D,所以AC⊥平面BDF.
因为EB⊥平面ABCD,FD⊥平面ABCD,所以EB∥FD.
所以B,D,F,E四点共面.
因为EF?平面BDFE,所以EF⊥AC.
解:(Ⅱ)设AC∩BD=O,连接EO,FO.
由(Ⅰ)知,AC⊥平面BDFE,
所以AC⊥平面FEO.
因为平面FEO将三棱锥E-FAC分为两个三棱锥A-FEO和C-FEO,
所以VE-FAC=VA-FEO+VC-FEO.
因为正方形ABCD的边长为a,$EB=2FD=\sqrt{2}a$,
所以$FO=\sqrt{F{D^2}+O{D^2}}=a$,$EO=\sqrt{E{B^2}+O{B^2}}=\frac{{\sqrt{10}}}{2}a$.
取BE的中点G,连接DG,则FE=DG=$\sqrt{D{B^2}+B{G^2}}=\frac{{\sqrt{10}}}{2}a$.
所以等腰三角形FEO的面积为${S_{△FEO}}=\frac{1}{2}a\sqrt{{{({\frac{{\sqrt{10}}}{2}a})}^2}-{{({\frac{1}{2}a})}^2}}$=$\frac{3}{4}{a^2}$.
所以VE-FAC=VA-FEO+VC-FEO=$\frac{1}{3}{S_{△FEO}}×AO+\frac{1}{3}{S_{△FEO}}×CO$=$\frac{1}{3}{S_{△FEO}}×AC$=$\frac{1}{3}×\frac{3}{4}{a^2}×\sqrt{2}a$=$\frac{{\sqrt{2}}}{4}{a^3}$.
所以三棱锥E-FAC的体积为$\frac{{\sqrt{2}}}{4}{a^3}$.
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,4) | B. | (-1,2) | C. | (2,4) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4) | B. | (4,14) | C. | (2,14) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 4 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com