
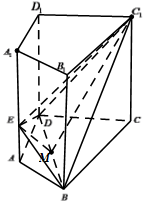
 如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.
如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.分析 (1)法一:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设M是BD的中点,连接MC1,利用向量法能证明平面EBD⊥平面C1BD.
法二:设M是BD的中点,连接EM和MC1,EC1,推导出∠EMC1是二面角E-BD-C1的平面角,由此能证明平面EBD⊥平面C1BD.
法三::以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设M是BD的中点,连接EM和MC1,EC1,则∠EMC1是二面角E-BD-C1的平面,由此能证明平面EBD⊥平面C1BD.
法四:连结AC,A1C1,B1D1,交点为O和N,以O为原点,OB为x轴,OC为y轴,ON为z轴,建立空间直角坐标系,利用向量法能证明平面EBD⊥平面C1BD.
(2)法一:求出平面C1DC的一个法向量和平面C1BD的法向量,利用向量法能求出二面角C-C1D-B的平面角的余弦值.
法二:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出二面角C-C1D-B的平面角的余弦值.
法三:设N是CD的中点,过N作NF⊥C1D于F,连接FB,则∠BFN是二面角C-C1D-B的平面角,由此能求出二面角C-C1D-B的平面角的余弦值.
解答 证明:(1)解法一:∵∠BCD=60°,$AB=AD=1,CB=CD=\sqrt{3}$,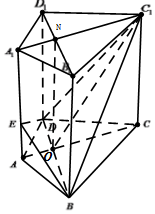
∴∠CDA=90°,∠CA=2…(1分)(没有这一步扣一分)
∴以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系…(2分)
设M是BD的中点,连接MC1…(2分)
∵C C1⊥平面ABCD,$CB=CD=\sqrt{3}$,∴C1D=C1B.
∵M是BD的中点,∴MC1⊥BD…(3分)
∵$E(1,0,\frac{{\sqrt{3}}}{4})$,$M(\frac{3}{4},\frac{{\sqrt{3}}}{4},0)$,${C_1}(0,\sqrt{3},\sqrt{3})$,
∴$\overrightarrow{M{C_1}}=(-\frac{3}{4},\frac{{3\sqrt{3}}}{4},\sqrt{3})$,$\overrightarrow{DE}=(1,0,\frac{{\sqrt{3}}}{4})$…(4分)∵$\overrightarrow{M{C_1}}•\overrightarrow{DE}=-\frac{3}{4}×1+\frac{{3\sqrt{3}}}{4}×0+\sqrt{3}×\frac{{\sqrt{3}}}{4}=0$,∴$\overrightarrow{M{C_1}}$⊥$\overrightarrow{DE}$…(5分)
(证得$\overrightarrow{M{C_1}}$⊥$\overrightarrow{ME}$或$\overrightarrow{BE}$也行)
∵$\overrightarrow{DE}$与BD相交于D,∴$\overrightarrow{M{C_1}}$⊥平面EBD.
∵$\overrightarrow{M{C_1}}$在平面C1BD内,∴平面EBD⊥平面C1BD…(6分)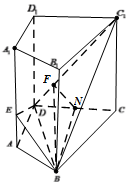
解法二:设M是BD的中点,连接EM和MC1,EC1…(1分)
∵AB=AD,CB=CD,∴BD⊥CA且C,A,M共线.∴BD⊥ME,BD⊥MC1.
∵EA⊥平面ABCD,C C1⊥平面ABCD,∴∠EMC1是二面角E-BD-C1的平面角…(2分)
∵∠BCD=60°,$AB=AD=1,CB=CD=\sqrt{3}$,
∴∠CDA=90°,$MA=\frac{1}{2},MC=\frac{3}{2}$…(3分)(正确计算出才给这1分)
∵A1E=3AE,$C{C_1}=\sqrt{3}$,∴$EM=\frac{{\sqrt{7}}}{4},{C_1}M=\frac{{\sqrt{21}}}{2}$.…(4分)(至少算出一个)
∵${C_1}E=\frac{{\sqrt{91}}}{4}$,…(5分)∴${C_1}{E^2}={C_1}{M^2}+E{M^2}$,即C1E⊥EM.
∴二面角E-BD-C1的平面角为直角.∴平面EBD⊥平面C1BD…(6分)
解法三:∵∠BCD=60°,$AB=AD=1,CB=CD=\sqrt{3}$,
∴∠CDA=90°,∠CA=2.
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系…(1分)
设M是BD的中点,连接EM和MC1,EC1..∵AB=AD,CB=CD,∴BD⊥CA且C,A,M共线…(2分)
∵EA⊥平面ABCD,C C1⊥平面ABCD,∴BD⊥ME,BD⊥MC1.
∴∠EMC1是二面角E-BD-C1的平面角…(3分)
则$E(1,0,\frac{{\sqrt{3}}}{4})$,${C_1}(0,\sqrt{3},\sqrt{3})$,$M(\frac{3}{4},\frac{{\sqrt{3}}}{4},0)$…(4分)(至少正确写出一个点的坐标)
∴$\overrightarrow{ME}=(\frac{1}{4},-\frac{{\sqrt{3}}}{4},\frac{{\sqrt{3}}}{4})$,$\overrightarrow{M{C_1}}=(-\frac{3}{4},\frac{{3\sqrt{3}}}{4},\sqrt{3})$.
∴$\overrightarrow{ME}•\overrightarrow{M{C_1}}=\frac{1}{4}×(-\frac{3}{4})+(-\frac{{\sqrt{3}}}{4})×\frac{{3\sqrt{3}}}{4}+\frac{{\sqrt{3}}}{4}×\sqrt{3}=0$…(5分)∴$\overrightarrow{ME}$⊥$\overrightarrow{M{C_1}}$,∠EMC1=90°,
二面角E-BD-C1的平面角为直角,平面EBD⊥平面C1BD…(6分)
解法四:连结AC,A1C1,B1D1,交点为O和N,如图.
∵∠BCD=60°,$AB=AD=1,CB=CD=\sqrt{3}$,∴∠CDA=90°,∠CA=2.
以O为原点,OB为x轴,OC为y轴,ON为z轴,建立空间直角坐标系…(1分)
则O是BD的中点.∵C C1⊥平面ABCD,$CB=CD=\sqrt{3}$,O是BD的中点,
∴C1D=C1B.∵O是BD的中点,∴OC1⊥BD…(3分)∵$E(0,-\frac{1}{2},\frac{{\sqrt{3}}}{4})$,$B(\frac{{\sqrt{3}}}{2},0,0)$,${C_1}(0,\frac{3}{2},\sqrt{3})$∴$\overrightarrow{O{C_1}}=(0,\frac{3}{2},\sqrt{3})$,$\overrightarrow{BE}=(-\frac{{\sqrt{3}}}{2},-\frac{1}{2},\frac{{\sqrt{3}}}{4})$.∵$\overrightarrow{O{C_1}}•\overrightarrow{BE}=-\frac{{\sqrt{3}}}{2}×0+\frac{3}{2}×(-\frac{1}{2})+\sqrt{3}×\frac{{\sqrt{3}}}{4}=0$,
∴$\overrightarrow{O{C_1}}$⊥$\overrightarrow{BE}$…(5分)∵$\overrightarrow{BE}$与BD相交于O,∴$\overrightarrow{O{C_1}}$⊥平面EBD.∵$\overrightarrow{O{C_1}}$在平面C1BD内,
∴平面EBD⊥平面C1BD…(6分)
解:(2)解法一:(若第1问已经建系)∵A(1,0,0),$\overrightarrow{DA}$⊥平面C1DC,
∴$\overrightarrow{DA}=(1,0,0)$是平面C1DC的一个法向量…(8分)
∵$B(\frac{3}{2},\frac{{\sqrt{3}}}{2},0)$,${C_1}(0,\sqrt{3},\sqrt{3})$,$\overrightarrow{DB}=(\frac{3}{2},\frac{{\sqrt{3}}}{2},0)$,$\overrightarrow{D{C_1}}=(0,\sqrt{3},\sqrt{3})$
设平面C1BD的法向量是$\overrightarrow m=(x,y,z)$,则$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{DB}=0\\ \overrightarrow m•\overrightarrow{D{C_1}}=0\end{array}\right.$,$\left\{\begin{array}{l}\frac{3}{2}x+\frac{{\sqrt{3}}}{2}y=0\\ \sqrt{3}y+\sqrt{3}z=0\end{array}\right.$,
取x=1,得$y=-\sqrt{3},z=\sqrt{3}$.平面C1BD的法量$\overrightarrow m=(1,-\sqrt{3},\sqrt{3})$…(10分)
【另解:由(1)知当A1E=3AE时,ME⊥平面C1BD,则平面C1BD的法向量是$\overrightarrow{ME}$=$(\frac{1}{4},-\frac{{\sqrt{3}}}{4},\frac{{\sqrt{3}}}{4})$】
∵$cos<\overrightarrow{DA},\overrightarrow m>=\frac{{\overrightarrow{DA}•\overrightarrow m}}{{|\overrightarrow{DA}|×|\overrightarrow m|}}$…(11分)=$\frac{{\sqrt{7}}}{7}$,
∴由图可知二面角C-C1D-B的平面角的余弦值为$\frac{{\sqrt{7}}}{7}$.…(12分)
解法二:(第1问未建系)∵∠BCD=60°,$AB=AD=1,CB=CD=\sqrt{3}$,∴∠CDA=90°,∠CA=2
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系…(7分)
∵A(1,0,0),$\overrightarrow{DA}$⊥平面C1DC,∴$\overrightarrow{DA}=(1,0,0)$是平面C1DC的法向量…(8分)
∵$B(\frac{3}{2},\frac{{\sqrt{3}}}{2},0)$,${C_1}(0,\sqrt{3},\sqrt{3})$,$\overrightarrow{DB}=(\frac{3}{2},\frac{{\sqrt{3}}}{2},0)$,$\overrightarrow{D{C_1}}=(0,\sqrt{3},\sqrt{3})$,
设平面C1BD的法向量是$\overrightarrow m=(x,y,z)$,则$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{DB}=0\\ \overrightarrow m•\overrightarrow{D{C_1}}=0\end{array}\right.$,$\left\{\begin{array}{l}\frac{3}{2}x+\frac{{\sqrt{3}}}{2}y=0\\ \sqrt{3}y+\sqrt{3}z=0\end{array}\right.$,
取x=1,得$y=-\sqrt{3},z=\sqrt{3}$.平面C1BD的法量$\overrightarrow m=(1,-\sqrt{3},\sqrt{3})$…(10分)
∵$cos<\overrightarrow{DA},\overrightarrow m>=\frac{{\overrightarrow{DA}•\overrightarrow m}}{{|\overrightarrow{DA}|×|\overrightarrow m|}}$…(11分)=$\frac{{\sqrt{7}}}{7}$.
∴由图可知二面角C-C1D-B的平面角的余弦值为$\frac{{\sqrt{7}}}{7}$.…(12分)
解法三:(几何法)
设N是CD的中点,过N作NF⊥C1D于F,连接FB,如图…(7分)
∠BCD=60°,$CB=CD=\sqrt{3}$,∴NB⊥CD.
∵侧面C1D⊥底面ABCD,∴NB⊥侧面C1D…(8分)
∵NF⊥C1D,∴BF⊥C1D∴∠BFN是二面角C-C1D-B的平面角…(9分)
∵依题意可得NB=$\frac{3}{2}$,NF=$\frac{{\sqrt{6}}}{4}$,BF=$\frac{{\sqrt{42}}}{4}$…(11分)
∴cos∠BFN=$\frac{NF}{BF}$=$\frac{{\sqrt{7}}}{7}$.∴二面角C-C1D-B的平面角的余弦值为$\frac{{\sqrt{7}}}{7}$.…(12分)
点评 本题考查面面垂直的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,考查创新意识、应用意识,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4) | B. | (4,14) | C. | (2,14) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 48种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com