
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 画出图形,数形结合判断命题P1;利用辅助角公式化积,求出x值判断命题P2;利用反证法证明命题P3.
解答 解:由f(x)=lgx-|x-2|=0,得lgx=|x-2|,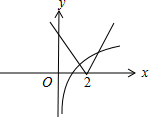
作出函数y=lgx,y=|x-2|的图象如图:
由图可知,两函数图象有两个交点,从而函数f(x)=lgx-|x-2|有2个零点,故P1为真命题;
∵sinx+$\sqrt{3}cosx=2sin(x+\frac{π}{3})=\sqrt{2}$,∴sin(x+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$,
∵x∈($\frac{π}{6}$,$\frac{π}{2}$),∴x+$\frac{π}{3}$∈($\frac{π}{2},\frac{5π}{6}$),则x+$\frac{π}{3}=\frac{3}{4}π$,即x=$\frac{5π}{12}$,故P2为真命题;
P3为真命题.用反证法证明如下:
假设a、b、c、d没有1个为负数,即a≥0、b≥0、c≥0、d≥0,∴ad+bc≥0,
∵a+b=c+d=2,∴(a+b)(c+d)=ac+bd+ad+bc=4,
∵ac+bd>4,∴ad+bc<0,这与ad+bc≥0矛盾,故P3为真命题.
∴正确命题的个数是3个.
故选:D.
点评 本题考查命题的真假判断与应用,考查函数零点个数的判定方法,训练了利用反证法证明不等式,是中档题.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ | B. | $\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | C. | $-\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | D. | $-\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
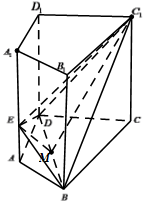 如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.
如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
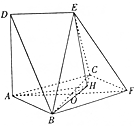 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${x^2}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | C. | ${x^2}-\frac{y^2}{6}=1$ | D. | $\frac{x^2}{{\frac{3}{2}}}-\frac{y^2}{{\frac{7}{2}}}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>$\frac{1}{3}$ | B. | b<$\frac{1}{3}$ | C. | b>$\frac{1}{2}$ | D. | b<$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com